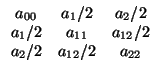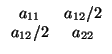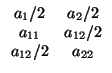Cónicas en el plano euclídeo

Una vez que hemos hecho todo el trabajo en dimensión cualquiera, la clasificación de la cuádricas en el plano euclídeo y en el espacio tridimensional, es muy sencilla. Sea C una cónica (que es, por definición, una cuádrica del plano). Escribimos su ecuación en una referencia ortonormal:

C $$\equiv$$ a₀₀ + a₁x + a₂y + a₁₁x² + a₁₂xy + a₂₂y² = 0.

Vamos a utilizar la siguiente notación:

$$\left(\vphantom{ \begin{array}{ccc} a_{00} & a_{1}/2 & a_{2}/2\\ a_{1}/2 & a_{11} & a_{12}/2\\ a_{2}/2 & a_{12}/2 & a_{22} \end{array} }\right. \begin{array}{ccc} a_{00} & a_{1}/2 & a_{2}/2\\ a_{1}/2 & a_{11} & a_{12}/2\\ a_{2}/2 & a_{12}/2 & a_{22} \end{array} \left.\vphantom{ \begin{array}{ccc} a_{00} & a_{1}/2 & a_{2}/2\\ a_{1}/2 & a_{11} & a_{12}/2\\ a_{2}/2 & a_{12}/2 & a_{22} \end{array} }\right) \left(\vphantom{ \begin{array}{cc} a_{11} & a_{12}/2\\ a_{12}/2 & a_{22} \end{array} }\right. \begin{array}{cc} a_{11} & a_{12}/2\\ a_{12}/2 & a_{22} \end{array} \left.\vphantom{ \begin{array}{cc} a_{11} & a_{12}/2\\ a_{12}/2 & a_{22} \end{array} }\right)$$

$$\widetilde{{A_{00}}} \left(\vphantom{ \begin{array}{cc} a_{1}/2 & a_{2}/2\\ a_{11} & a_{12}/2\\ a_{12}/2 & a_{22} \end{array} }\right. \begin{array}{cc} a_{1}/2 & a_{2}/2\\ a_{11} & a_{12}/2\\ a_{12}/2 & a_{22} \end{array} \left.\vphantom{ \begin{array}{cc} a_{1}/2 & a_{2}/2\\ a_{11} & a_{12}/2\\ a_{12}/2 & a_{22} \end{array} }\right)$$

Para decir el tipo de cónica que se tiene, hay que estudiar los distintos rangos y signaturas.

Nota 4.2.1   Utilizamos el siguiente convenio: si la ecuación reducida de C es

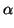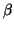A + cy + $$\alpha$$x² + $$\beta$$y²,

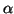
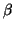
supondremos que en los signos de $\alpha$ y $\beta$ hay al menos tantos positivos como negativos. Si al hacer el estudio de una cónica nos salen los dos negativos o que uno es negativo y el otro cero, el razonamiento es el mismo, pero al final se cambia de signo la ecuación reducida para saber el tipo de C.

Paso 1: Rango de A₀₀. Conocer esto nos dice si en la ec. reducida vamos a tener $\alpha$ y $\beta$ distintos de cero, o sólo uno de ellos.

1. rg(A₀₀) = 2. De aquí deducimos (evidentemente) que el rango de $\widetilde{{A_{00}}}$ es también 2 y que, por tanto, en la ecuación reducida se tiene c = 0. Estudiamos la signatura de A₀₀.
   1. sign(A₀₀) = 2. Esto quiere decir que los autovalores de A₀₀ son ambos positivos. Por tanto, la ecuación reducida será de la forma:
      A +|$$\alpha$$|x² +|$$\beta$$|y² = 0.
      Para conocer el signo de A, puesto que $\alpha$ y $\beta$ son distintos de 0, basta conocer el valor del determinante de M, pues det(M) = $\alpha$$\beta$A.
      1. det(M) < 0. En este caso, A < 0 y la ecuación reducida es
         -|A|+|$$\alpha$$|x² +|$$\beta$$|y² = 0,
         que es una elipse real.
      2. det(M) = 0. La ecuación reducida es
         |$$\alpha$$|x² +|$$\beta$$|y² = 0,
         que es un par de rectas imaginarias secantes.
      3. det(M) > 0. Entonces A > 0 y la ec. red. es
         |A|+|$$\alpha$$|x² +|$$\beta$$|y² = 0,
         que es una elipse imaginaria.
   2. sign(A₀₀) = 1. De aquí se deduce que $\alpha$ > 0 y $\beta$ < 0 (o al revés). En esta situación da igual que el valor de A sea positivo o negativo: sólo interesa si es nulo o no.
      1. det(M) $\neq$ 0. La ecuación reducida es
         A +|$$\alpha$$|x² -|$$\beta$$|y² = 0
         (o con los signos de $\alpha$ y $\beta$ cambiados. Esto es una hipérbola.
      2. det(M) = 0. Entonces la ec. red. es
         |$$\alpha$$|x² -|$$\beta$$|y² = 0,
         (ibid.) que es un par de rectas reales secantes.
   3. Si la signatura de A₀₀ es 0 (dos autovalores negativos), se estudia el signo de det(M) como en los casos anteriores, para conocer el signo de A. Se escribe la ecuación reducida y se cambia de signo. Con esto, se llega a una del tipo ``elipse''.
2. rg(A₀₀) = 1. Esto quiere decir que $\alpha$ $\neq$ 0 y $\beta$ = 0 (o al revés, da igual). Aquí hay que estudiar el rango de $\widetilde{{A_{00}}}$.
   1. rg($\widetilde{{A_{00}}}$) = 2. La única posibilidad es que la ecuación reducida sea del tipo
      cy + $$\alpha$$x² = 0,
      donde los signos son irrelevantes. Esto es una parábola.
   2. rg($\widetilde{{A_{00}}}$) = 1. Hay que conocer el rango de M y alguna cosa más.
      1. rg(M) = 2. Hay dos posibilidades (que hay que comprobar ``a mano''):

         a)

         Si C tiene puntos, entonces la ec. reducida es -|A|+ $\alpha$x² = 0, que es un par de rectas reales paralelas.

         b)

         Si C no tiene puntos, entoneces la ec. red. es |A|+ $\alpha$x² = 0, que es un par de rectas paralelas imaginarias.

      2. rg(M) = 1. La ec. reducida es
         $$\alpha$$x² = 0,
         que es una recta doble.

Se deduce la siguiente tabla (donde c = 0 quiere decir que rg($\widetilde{{A_{00}}}$) = rg(A₀₀) y c $\neq$ 0, que rg($\widetilde{{A_{00}}}$) > rg(A₀₀)):

rg(A₀₀) = 2

sign(A₀₀) = 2

|-| det(M) < 0	elipse real
|-| det(M) = 0	rectas complejas secantes
|-| det(M) > 0	elipse imaginaria

sign(A₀₀) = 1

|-| det(M) $\neq$ 0	hipérbola
|-| det(M) = 0	rectas reales secantes

sign(A₀₀) = 0

|-|	cámbiese el signo

rg(A₀₀) = 1

sign(A₀₀) = 1

|-| rg($\widetilde{{A_{00}}}$) = 2	parábola
|-| rg(M) = 2	con puntos: rec. par. real.
|-| rg(M) = 1	recta doble
|-| rg(M) = 2	sin puntos: rec. par. imag.

sign(A₀₀) = 0

|-|	cámbiese el signo
|-|

La tabla clasificatoria de cuádricas está por hacer. Lo lamento, espero tener tiempo en breve para incluirla.

Gracias por la comprensión.