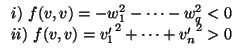Next: Formas bilineales simétricas definidas
Up: Clasificación de las formas
Previous: Clasificación de las formas
TEOREMA 1.4.1
Dos formas bilineales simétricas sobre
V, un
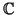
-espacio vectorial de dimensión finita, que
tienen el mismo rango, difieren en un cambio de base (y, evidentemente, si difieren en un cambio de base,
tienen el mismo rango).
Demostración.
Por lo que se vió en la sección anterior, una forma bilineal simétrica sobre
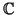
admite
siempre una base ortogonal. Sean
f1 y
f2 dos formas bilineales simétricas sobre
V, que tengan el
mismo rango
r. Sea

= (
e1,...,
en) una base ortogonal y ``normalizada'' para
f1: es
decir, la matriz de
f1 en

es:
En esa misma base, la matriz de
f2 será
M2. Pero sabemos que existe un cambio de base que
transforma la matriz
M2 en
M1. Es decir:
M1 = NtM1N
que es precisamente, decir que difieren en un cambio de base.

Sobre
 , las cosas cambian un poco, porque no tenemos raíces cuadradas. (Y lo mismo pasa para
las formas hermíticas):
, las cosas cambian un poco, porque no tenemos raíces cuadradas. (Y lo mismo pasa para
las formas hermíticas):
TEOREMA 1.4.2
Sea
f :
V×
V una forma bilineal simétrica sobre

(o una forma hermítica). Sea
r =
rg(
f ). Existen naturales
p,
q con
p +
q =
r y una base

= (
e1,...,
ep,
ep+1,...,
ep+q,
ep+q+1,...,
en) tales que la matriz de
f en dicha base
es:
Demostración.
En la sección anterior se demostró que existe una base ortogonal para
f, así que la tomamos:

= (
e1,...,
en). La ordenamos de la siguiente manera: sea
p el número de vectores de

tales que
f (
e,
e) > 0. Sea
q el número de vectores tales que
f (
e,
e) < 0.
Para
i = 1...p + q, tomamos
e'i = 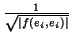 ei. Es claro que, en esta
nueva base, la matriz tiene la forma pedida. (Los vectores de ker(f ) no se tocan porque anulan a todos y a
sí mismos).
ei. Es claro que, en esta
nueva base, la matriz tiene la forma pedida. (Los vectores de ker(f ) no se tocan porque anulan a todos y a
sí mismos).

Se tiene, de hecho, el siguiente resultado, para clasificar las formas bilineales simétricas sobre
 :
:
TEOREMA 1.4.3 (Teorema de inercia de Steiner)
Si
f es una forma bilineal simétrica sobre un

-espacio vectorial
V, entonces el
número de +1 y el número de -1 de la matriz de
f en cualquier base que satisfaga la tesis del
teorema anterior es el mismo. Es decir,
p y
q son invariantes
de la forma. A la matriz escrita
arriba se le llama
forma canónica de f.
HASTA AQUÍ LA CLASE 6 990222
Demostración.
Podemos suponer que la forma es no degenerada, porque el rango es invariante y nos restringimos a un
subespacio complementario del ker(
f ). Supongamos, para llegar a una contradicción, que existen bases

= (
e1,...,
ep,
f1,...,
fq) y


(
e'1,...,
e'p',
f'1,...,
f'q') tales que
p <
p' (y, por tanto,
q >
q'). Como
p +
q =
n y
p' +
q' =
n y, además,
p <
p', resulta que
p' +
q >
n y, por la fórmula de las dimensiones, debe existir un
vector
v 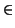
<
e'1,...,
e'p' >
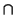
<
f1,...,
fq > .
Calculando, si
v = (0,..., 0,
w1,...,
wq) en la base

y
v = (
v'1,...,
v'p, 0,..., 0) en la base


que es, como todo el mundo sabe, una contradicción.

COROLARIO 1.4.4
Dos formas bilineales simétricas sobre un

-espacio vectorial difieren en un cambio de base si y
sólo si tienen el mismo número de +1 y -1 en sus formas canónicas.
Definición 1.4.5
El número p se llama signatura de f. El teorema de Steiner se enuncia diciendo que dos formas
bilineales simétricas difieren en un cambio de base si y sólo si tienen mismo rango y misma signatura.



Next: Formas bilineales simétricas definidas
Up: Clasificación de las formas
Previous: Clasificación de las formas
Pedro Fortuny Ayuso
2001-06-15


![]() ei. Es claro que, en esta
nueva base, la matriz tiene la forma pedida. (Los vectores de ker(f ) no se tocan porque anulan a todos y a
sí mismos).
ei. Es claro que, en esta
nueva base, la matriz tiene la forma pedida. (Los vectores de ker(f ) no se tocan porque anulan a todos y a
sí mismos).
![]()
![]() :
: