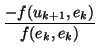Formas bilineales simétricas definidas

Vamos a dar un procedimiento constructivo de una base ortogonal (ortonormal, en su caso) para una forma bilineal simétrica definida. En este apartado suponemos siempre que el cuerpo base es $\mathbb {R}$.

TEOREMA 1.4.6   Sea V un espacio vectorial real de dimensión n y (u₁,..., u_n) una base. Sea f : V×V $\rightarrow$ $\mathbb {R}$ una forma bilineal simétrica definida. Entonces existe una base (e₁,..., e_n) de V tal que:

• < e₁,..., e_k > = < u₁,..., u_k > para k = 1...n.
• (e₁,..., e_n) es una base ortogonal para f.

Demostración. La demostración es constructiva: Tomamos, como f es no degenerada -pues es definida-, el vector e₁ = u₁, sin más preámbulos.

Supongamos que hemos construido k vectores (e₁,..., e_k) que cumplen las condiciones. Vamos a construir el siguiente: tiene que ser

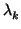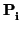e_k+1 = u_k+1 + $$\lambda_{{k}}^{}$$e_k + ... + $$\lambda_{{1}}^{}$$e₁

(se pone u_k+1 con coeficiente 1, pero podría tomarse cualquier otro coeficiente no nulo). Ahora le imponemos las condiciónes de ortogonalidad con los demás:

$$\left\{\vphantom{ \begin{array}{l} f(e_{k+1},e_{1})=f(u_{k+1},e_{... ..._{k+1},e_{k})=f(u_{k+1},e_{k})+\lambda _{k}f(e_{k},e_{k})=0 \end{array}}\right.$$$$\begin{array}{l} f(e_{k+1},e_{1})=f(u_{k+1},e_{1})+\lambda _{1}f(... ...\\ f(e_{k+1},e_{k})=f(u_{k+1},e_{k})+\lambda _{k}f(e_{k},e_{k})=0 \end{array}$$

que me dicen que

$$\lambda_{{1}}^{}$$ = $${\frac{{-f(u_{k+1},e_{1})}}{{f(e_{1},e_{1})}}}$$, ..., $$\lambda_{{k}}^{}$$ = $${\frac{{-f(u_{k+1},e_{k})}}{{f(e_{k},e_{k})}}}$$

que tiene sentido porque los denominadores no son nulos, pues la forma es definida. Y, con este procedimiento, se consiguen n vectores ortogonales dos a dos, que son una base, y que cumplen la condición:

< e₁,..., e_k > = < u₁,..., u_k >     parak = 1...n,

como se pedía. $\qedsymbol$

COROLARIO 1.4.7 (Teorema de Gram-Schmidt)   Si f es definida positiva y el conjunto (u₁,..., u_n) es una base de V, entonces existe una base ortonormal (e₁,..., e_k) de V tal que, para k = 1...n, se tiene

< e₁,..., e_k > = < u₁,..., u_k >     parak = 1...n.

Demostración. Tómese la base ortogonal construida en el teorema anterior y normalícese como sigue:

e'_i = $${\frac{{1}}{{\sqrt{f(e_{i},e_{i})}}}}$$.

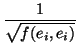
La raíz cuadrada tiene sentido porque la forma es definida positiva. $\qedsymbol$

HASTA AQUÍ LA CLASE 7 990223. LO DEMÁS SE EXPLICÓ EN PROBLEMAS.
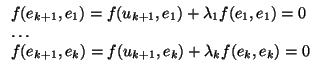
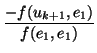