


Next: ESPACIO AFÍN
Up: Clasificación de las formas
Previous: Componentes horizontal y vertical
Vamos a enunciar los mismos resultados para formas cuadráticas.
Definición 1.4.9
Sea
V un
K -espacio vectorial.
- Dos formas cuadráticas
Q1, Q2 : V
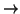 K son linealmente equivalentes si existe un
automorfismo
K son linealmente equivalentes si existe un
automorfismo
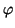 : V
: V 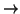 V tal que
Q1(v) = Q2(
V tal que
Q1(v) = Q2(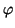 (v)). Que es lo mismo que decir que
difieren en un cambio de base.
(v)). Que es lo mismo que decir que
difieren en un cambio de base.
- Se llama rango de una forma cuadrática Q al de fQ. Si V es un espacio vectorial real,
se llama signatura de Q a la de fQ.
PROPOSICIÓN 1.4.10
Se tienen los siguientes resultados:
- Si V es un espacio vectorial sobre
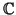 , dos formas cuadráticas son linealmente
equivalentes si y sólo si tienen el mismo rango.
, dos formas cuadráticas son linealmente
equivalentes si y sólo si tienen el mismo rango.
- Si V es un espacio vectorial sobre
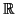 , dos formas cuadráticas son linealmente
equivalentes si y sólo si tienen mismo rango y misma signatura.
, dos formas cuadráticas son linealmente
equivalentes si y sólo si tienen mismo rango y misma signatura.
La demostración es que estos enunciados se refieren a formas bilineales asociadas, para los que ya se han
probado.
Definición 1.4.11
Sea
V un
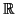
-espacio vectorial y
Q una forma cuadrática sobre
V. Se dice que
Q es definida
cuando
fQ lo es, es decir, si
Q(
u)
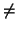
0 para todo
u  V
V,
u 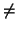
0. Si
Q es una forma definida, se
dice que es definida positiva cuando
Q(
u) > 0 para todo
u 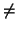
0 y se dice que es definida negativa si
Q(
u) < 0 para todo
u 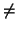
0.
Demostración.
La demostración de la primera afirmación ya se ha hecho con las formas bilineales simétricas. La de la
segunda,
se deja como ejercicio que conviene hacer.
Nota 1.4.13
Para formas hermíticas también se definen el rango y la signatura, con +1 y -1 y se demuestra un
teorema que tiene el mismo enunciado que el de Steiner: dos formas hermíticas difieren en un cambio de
base si y sólo si tienen el mismo rango y la misma signatura.
Se acabó el tema de las formas bilineales en estado puro. Empezaremos con los espacios afín y
métrico.



Next: ESPACIO AFÍN
Up: Clasificación de las formas
Previous: Componentes horizontal y vertical
Pedro Fortuny Ayuso
2001-06-15
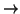 K son linealmente equivalentes si existe un
automorfismo
K son linealmente equivalentes si existe un
automorfismo
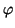 : V
: V 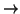 V tal que
Q1(v) = Q2(
V tal que
Q1(v) = Q2(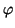 (v)). Que es lo mismo que decir que
difieren en un cambio de base.
(v)). Que es lo mismo que decir que
difieren en un cambio de base.