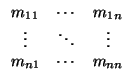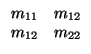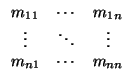La manera de calcularla es simple. Se resuelva un sistema o, mejor (para mí), calcúlese una base
ortogonal de
f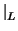 , extiéndase a una base de todo el espacio y termínese. (Evidentemente, si uno
conoce vL, conoce
vL
, extiéndase a una base de todo el espacio y termínese. (Evidentemente, si uno
conoce vL, conoce
vL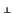 , no hay más que poner
vL
, no hay más que poner
vL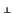 = v - vL.
= v - vL.
Nota 1.4.8
Sobre los determinantes de Gram. Dada una forma bilineal simétrica definida, su matriz en una base se
escribirá:
Se tiene lo siguiente (independientemente de la base):
- f es definida positiva si y sólo si lo menores de la diagonal son todos positivos:
det(
m11) =
m11 > 0, det

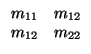

> 0 det

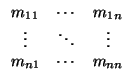

> 0.
- f es definida negativa si y sólo si esos mismos determinantes tienen signos alternados, comenzando
por
det(m11) = m11 < 0, el siguiente positivo, el siguiente negativo...
Esos determinantes se llaman
determinantes de Gram respecto de la base
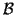
. Este resultado se
aplica, palabra por palabra, a las formas cuadráticas, construyendo la matriz de la forma bilineal asociada.
![]() , extiéndase a una base de todo el espacio y termínese. (Evidentemente, si uno
conoce vL, conoce
vL
, extiéndase a una base de todo el espacio y termínese. (Evidentemente, si uno
conoce vL, conoce
vL![]() , no hay más que poner
vL
, no hay más que poner
vL![]() = v - vL.
= v - vL.