


Next: Referencia en un espacio
Up: El espacio afín
Previous: El espacio afín
Fijemos un espacio vectorial V de dimensión finita n sobre un cuerpo K (que, como es habitual, será
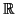 ó
ó
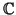 ). Sea
). Sea
 un conjunto cualquiera, a cuyos elementos denominaremos
puntos. Diremos que la terna
(
un conjunto cualquiera, a cuyos elementos denominaremos
puntos. Diremos que la terna
( , V, +) es un espacio afín si + es una aplicación
, V, +) es un espacio afín si + es una aplicación
que cumple las siguientes condiciones:
- Dados dos puntos
 ,
,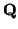 , existe un vector v
, existe un vector v  V tal que
V tal que
 + v =
+ v = 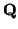 .
.
- Dado un punto


 , se tiene que
, se tiene que
 + v =
+ v =  si y sólo si v = 0.
si y sólo si v = 0.
- Dados un punto


 y dos vectores v, w
y dos vectores v, w  V, es
(
V, es
( + v) + w =
+ v) + w =  + (v + w).
+ (v + w).
Es importante tener una idea geométrica de lo que estamos diciendo:
 es el conjunto de puntos del espacio, mientras que V es el espacio vectorial obtenido a partir de todos los vectores fijos
que se pueden construir en
es el conjunto de puntos del espacio, mientras que V es el espacio vectorial obtenido a partir de todos los vectores fijos
que se pueden construir en
 , módulo la relación de equipolencia (tener misma dirección y
sentido). Es decir, cuando
, módulo la relación de equipolencia (tener misma dirección y
sentido). Es decir, cuando
 es el conjunto de puntos del espacio, V es el espacio vectorial
es el conjunto de puntos del espacio, V es el espacio vectorial
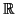 3. Puede ayudar pensar que entendemos
3. Puede ayudar pensar que entendemos
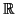 3 de dos formas diferentes: por un lado,
como conjunto de puntos -que, de momento, no tienen ni coordenadas ni nada- y por otro, como el espacio
vectorial que sería un conjunto de vectores que parten de un mismo sitio: el vector 0.
3 de dos formas diferentes: por un lado,
como conjunto de puntos -que, de momento, no tienen ni coordenadas ni nada- y por otro, como el espacio
vectorial que sería un conjunto de vectores que parten de un mismo sitio: el vector 0.
A partir de ahora, denotaremos por 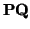 al vector v (que es único) tal que
al vector v (que es único) tal que
 + v =
+ v = 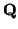 .
.
Propiedades que se deducen de la definición:
- Dados dos puntos
 ,
,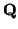

 , el vector
, el vector 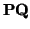 (es decir, el único v
(es decir, el único v  V
tal que
V
tal que
 + v = Q) es 0 si y sólo si
+ v = Q) es 0 si y sólo si
 =
= 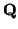 .
.
- Dados tres puntos
 ,
,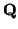 ,
,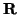

 , se tiene que
, se tiene que
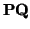 +
+ 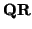 =
= 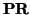 .
.
- Si
 y
y 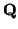 son dos puntos, entonces
son dos puntos, entonces
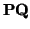 = -
= - 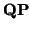 .
.
- Sean
 y
y 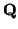 dos puntos y v, w dos vectores. Tomemos
dos puntos y v, w dos vectores. Tomemos
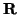 =
=  + v,
+ v,
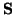 =
= 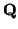 + w. Entonces
+ w. Entonces
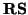 =
= 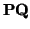 + w - v.
+ w - v.
- En general, si K es un cuerpo, el conjunto Kn se puede entender como un espacio afín sobre
el espacio vectorial Kn, donde la operación de sumar puntos con vectores es la natural: dados un punto
 = (p1,..., pn) y un vector
(v1,..., vn), se define
= (p1,..., pn) y un vector
(v1,..., vn), se define
 + v = (p1 + v1,..., pn + vn).
+ v = (p1 + v1,..., pn + vn).



Next: Referencia en un espacio
Up: El espacio afín
Previous: El espacio afín
Pedro Fortuny Ayuso
2001-06-15
![]() ó
ó
![]() ). Sea
). Sea
![]() un conjunto cualquiera, a cuyos elementos denominaremos
puntos. Diremos que la terna
(
un conjunto cualquiera, a cuyos elementos denominaremos
puntos. Diremos que la terna
(![]() , V, +) es un espacio afín si + es una aplicación
, V, +) es un espacio afín si + es una aplicación
![]() al vector v (que es único) tal que
al vector v (que es único) tal que
![]() + v =
+ v = ![]() .
.