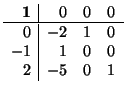Next: Subespacios de un espacio
Up: El espacio afín
Previous: Definición y propiedades básicas
De ahora en adelante,
 será un espacio afín sobre un espacio vectorial V, que
supondremos de dimensión n.
será un espacio afín sobre un espacio vectorial V, que
supondremos de dimensión n.
Definición 2.1.1
Una
referencia en

es una familia

= (

,(
e1,...,
en)), donde

es un elemento de

-es decir, un punto- y
(
e1,...,
en) es una base de
V. Al punto

se le denomina
origen de coordenadas.
Si fijamos una referencia
 como arriba, a todo punto
como arriba, a todo punto  del espacio afín
del espacio afín
 podemos asociarle una n -upla, que denominaremos coordenadas de
podemos asociarle una n -upla, que denominaremos coordenadas de  en la referencia
en la referencia
 , de la siguiente forma: tomamos el vector
, de la siguiente forma: tomamos el vector 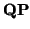 y calculamos sus coordenadas en la base
(e1,..., en), digamos
y calculamos sus coordenadas en la base
(e1,..., en), digamos
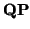 = (
= (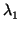 ,...,
,...,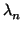 ). La matriz (vector)
(
). La matriz (vector)
(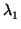 ,
,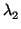 ,...,
,...,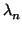 ) son las coordenadas de
) son las coordenadas de  en la referencia
en la referencia
 . Es
claro que si
. Es
claro que si


 tiene coordenadas
(p1,..., pn) en la referencia
tiene coordenadas
(p1,..., pn) en la referencia
 y v
y v  V tiene coordenadas
(v1,..., vn) en la base
(e1,..., en), entonces el punto
V tiene coordenadas
(v1,..., vn) en la base
(e1,..., en), entonces el punto
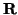 =
=  + v tiene coordenadas
(r1,..., rn) con
r1 = p1 + v1,..., rn = pn + vn.
+ v tiene coordenadas
(r1,..., rn) con
r1 = p1 + v1,..., rn = pn + vn.
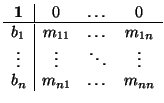
PROPOSICIÓN 2.1.2 (Fórmulas del cambio de referencia)
Tomemos dos referencias

= (
O,(
e1,...,
en)) y


= (
O',(
e'1,...,
e'n)) en el espacio afín
(

,
V). Sean
(
p1,...,
pn) las coordenadas de un punto

en la referencia

y
(
p'1,...,
p'n) las coordenadas del mismo punto

en la referencia


. Sea
M = (
mij) la matriz de cambio de base de
(
e1,...,
en) a
(
e'1,...,
e'n) -es decir,
e'i =
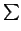 mjiej
mjiej (
ojo a los subíndices mji). Entonces
donde
(
b1,...,
bn) son las coordenadas de
O' en la referencia

.
Demostración.
Se trata de una mera comprobación. Por las propiedades de los espacios afines, sabemos que
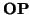
=
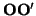
+
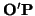
. Es decir,
de donde, como (
mij) es la matriz de cambio de base de
(
e1,...,
en) a
(
e'1,...,
e'n), se
deduce que
que, matricialmente se escribe
y esta expresión se resume en la del enunciado. (Que conviene utilizar siempre, pues así uno distingue
cuándo está utilizando un ``mero'' espacio vectorial y un ``complicado'' espacio afín. (por los
)).

Ejemplo. Tomemos el espacio afín de los puntos del espacio (que para entendernos, denotaremos
 =
=  3). El espacio vectorial subyacente V es el espacio vectorial real
3). El espacio vectorial subyacente V es el espacio vectorial real
 3. Tomemos una referencia
3. Tomemos una referencia
 , formada por un punto cualquiera
, formada por un punto cualquiera
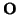

 y la
base canónica de
V =
y la
base canónica de
V =  3 (cuyos elementos llamamos ei). Tomemos otra referencia
3 (cuyos elementos llamamos ei). Tomemos otra referencia

 , formada por otro punto O' (cuyas coordenadas en la referencia
, formada por otro punto O' (cuyas coordenadas en la referencia
 son
O' = (1, 2, 3)) y la
base de V dada por
(e'1, e'2, e'3) con
e'1 = (0, 1, 0),
e'2 = (1, 2, 5),
e'3 = (0, 0, 1). Sea
ahora
son
O' = (1, 2, 3)) y la
base de V dada por
(e'1, e'2, e'3) con
e'1 = (0, 1, 0),
e'2 = (1, 2, 5),
e'3 = (0, 0, 1). Sea
ahora  un punto cualquiera de
un punto cualquiera de
 . Supongamos que las coordenadas de
. Supongamos que las coordenadas de  en la
referencia
en la
referencia

 son
(p'1, p'2, p'3). Cambiemos de referencia. No hay más que aplicar la
fórmula. Si las coordenadas de
son
(p'1, p'2, p'3). Cambiemos de referencia. No hay más que aplicar la
fórmula. Si las coordenadas de  en la referencia
en la referencia
 son
(p1, p2, p3), entonces
Los
son
(p1, p2, p3), entonces
Los 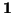 en negrita son los ``espurios''.
en negrita son los ``espurios''.
En realidad, esa forma matricial la vamos a utilizar casi sólo en la teoría. Cuando uno se enfrenta a
un problema, da igual poner la matriz grande (con los 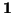 ) o usar la pequeña y sumar las corrdenadas
del punto. Lo importante es el resultado final y que el razonamiento sea correcto.
) o usar la pequeña y sumar las corrdenadas
del punto. Lo importante es el resultado final y que el razonamiento sea correcto.
Si el problema que se plantea es ``calcular el cambio de referencia de
 a
a

 ,
necesitamos hacer lo siguiente:
,
necesitamos hacer lo siguiente:
Primero: calculamos la matriz (nij) inversa de (mij), en nuestro caso, (nij) es
que es la matriz de cambio de base de
(e'1, e'2, e'3) a
(e1, e2, e3).
Segundo: calculamos las coordenadas del vector
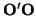 = -
= - 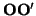 en la nueva base. Para ello hay
que cabiar de base dicho vector, que es
(- 1, - 2, - 3) en la base de las ei:
en la nueva base. Para ello hay
que cabiar de base dicho vector, que es
(- 1, - 2, - 3) en la base de las ei:
Tercero: aplicamos la fórmula. Si
(p'1, p'2, p'3) son las coordenadas de P en la
referencia

 , es
, es



Next: Subespacios de un espacio
Up: El espacio afín
Previous: Definición y propiedades básicas
Pedro Fortuny Ayuso
2001-06-15
![]() será un espacio afín sobre un espacio vectorial V, que
supondremos de dimensión n.
será un espacio afín sobre un espacio vectorial V, que
supondremos de dimensión n.
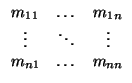

![]() ) o usar la pequeña y sumar las corrdenadas
del punto. Lo importante es el resultado final y que el razonamiento sea correcto.
) o usar la pequeña y sumar las corrdenadas
del punto. Lo importante es el resultado final y que el razonamiento sea correcto.
![]() a
a
![]()
![]() ,
necesitamos hacer lo siguiente:
,
necesitamos hacer lo siguiente:
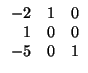
![]() = -
= - ![]() en la nueva base. Para ello hay
que cabiar de base dicho vector, que es
(- 1, - 2, - 3) en la base de las ei:
en la nueva base. Para ello hay
que cabiar de base dicho vector, que es
(- 1, - 2, - 3) en la base de las ei:
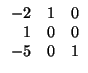
![]()
![]() , es
, es