Nota 3.1.1 (Importante)
En todo lo que sigue de estos apuntes, cuando aparece una expresión
donde
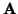
y
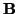
son puntos, se entiende que es el vector que va de
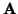
a
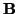
, es
decir, el único vector
v tal que
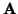
+
v =
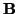
. Esto es distinto de lo que hemos hecho en clase
(siempre poníamos una barra encima:
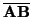
). Lo he dejado así porque está claro por
el contexto y porque hay que acostumbrarse a leer las cosas sin que lo expliquen todo. Por ejemplo, si
f es
una afinidad y
f (
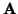
) y
f (
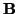
) son las imágenes de los puntos
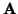
y
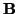
, entonces
f (
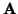
)
f (
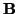
) es el vector
w tal que
f (
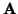
) +
w =
f (
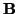
).