Breve descripción de la noción de grupo

Un grupo es una familia de cosas en la que tiene sentido hablar de ``tomar'' (``coger'', ``usar'') primero una y después otra, de manera que cada ``toma'' puedo deshacerla y que si ``tomo una, luego otra y con el resultado tomo otra'' es lo mismo que ``tomar una y a este resultado aplicarle el tomar ``la segunda y la tercera de antes''''. Bien, no está nada claro. Un grupo es un par (G, +) formado por un conjunto G y un aplicación

G×G	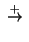$$\;\stackrel{{+}}{{\rightarrow}}\;$$	G
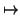(a, b)	$$\mapsto$$	a + b

que se llama ``operación del grupo'' y que cumple:

• (a+b)+c=a+(b+c)
• Existe un elemento e $\in$ G tal que a + e = e + a = a para todo a $\in$ G.
• Para cada a $\in$ G existe un a' $\in$ G tal que a + a' = a' + a = e.

Es importante darse cuenta de que no se exige la conmutatividad. Los grupos que cumplen a + b = b + a se llaman conmutativos o abelianos. Y los que vamos a estudiar en este curso no lo son, habitualmente.