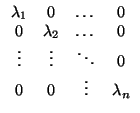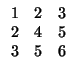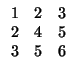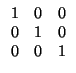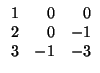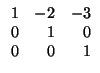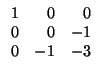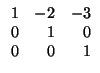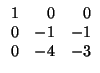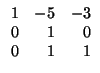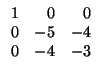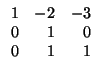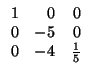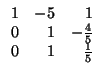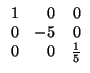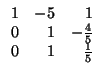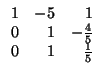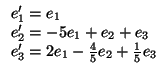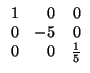Next: Clasificación de las formas
Up: FORMAS BILINEALES
Previous: Propiedades del ortogonal.
Cuando se estudió la clasificación de endomorfismos de Jordan, lo que se pretendía era conseguir una
matriz lo más simple posible para una aplicación lineal. Una de las utilidades que tiene es, por ejemplo,
el cálculo de las exponenciales de matrices: ¿qué significa, si M es una matriz, la expresión
eM?
y ¿cómo se calcula?. Uno puede hacerlo a lo bruto con el desarrollo de potencias siguiente:
eM =
Id +
M +
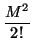
+
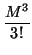
+ ... +
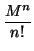
+ ...
pero, aparte de ser tedioso, es de locos. Y ponte a calcular Mn... Sin embargo, si expresamos el morfismo
con una base de Jordan, sabemos que hay matrices P, M', N con P invertible, M' diagonal y N nilpotente
(i.e. Nk = 0 para k > > 0) tales que
M = P-1(M' + N)P
de donde, si la exponencial cumple lo que debe cumplir, ha de ser (utilizando, también, que M' y N
conmutan):
eM = P-1eM'eNP,
y ahora, la exponencial de una matriz diagonal no es más que la matriz diagonal con los elementos
``exponenciados'' y el desarrollo de eN es finito (hasta que Nk se anula). Esto es útil para las
soluciones de los sistemas de ecuaciones diferenciales lineales.
En este apartado vamos a estudiar la diagonalización de la matriz de una forma bilineal simétrica. Primera cosa importante que hay que tener en la cabeza: cuando trabajamos con formas bilineales
no estamos trabajando con endomorfismos, por lo tanto, el cambio de base de una forma bilineal no se
comporta como el cambio de base de un endomorfismo. No hay P-1 porque ``ni entramos ni salimos del
espacio''. Hay P y Pt porque ``escribimos los vectores en otra base''. Esto, aunque ahora -que no vamos
a meter endomorfismos para nada- esté claro, hay que tenerlo también claro cuando estudiemos el espacio
euclídeo, en el que mezclaremos formas bilineales (los productos escalares) y endomorfismos (los
movimientos).
Vamos ya con las definiciones y resultados sobre diagonalización de matrices de formas bilineales simétricas. Fijamos un espacio vectorial de dimensión n, llamémosle V, y una forma bilineal
simétrica
f : V×V 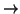 K.
K.
Definición 1.3.1
Una base

= (
e1,...,
en) de
V se llama
ortogonal para f si la matriz de
f en la
base

es diagonal. Se dice que

es
ortonormal si es
f (
ei,
ej) =
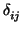
(
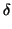
de Kronecker ).
Está claro que una base ortogonal es una base formada por vectores ortogonales dos a dos. Para la ortonormal
se pide,además, que ``el módulo'' (ya lo veremos) de cada vector sea 1.
Nota 1.3.2
Sea

es una base ortogonal. Si tomamos
e'i =
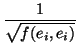 ei
ei,
entonces la base


= (
e'1,...,
e'n) es ortonormal. Esto sólo lo podemos hacer si
f (
ei,
ei)
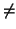
0 y el cuerpo
K =
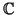
o, si
K =

y
f (
ei,
ei) > 0 para todo
i. Es
decir, si
f es no degenerada en el caso complejo y si es definida positiva en el caso real.
TEOREMA 1.3.3
Dada una forma bilineal simétrica
f sobre un e.v. de dimensión finita, existe una base

ortogonal para
f.
HASTA AQUÍ LA CLASE 5: 990219
Demostración.
Primero: la forma bilineal puede ser la nula:
f (
u,
v) = 0
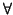 u
u,
v  V
V. En este caso, comprobáis
inmediatamente que cualquier matriz de
f es diagonal (de hecho es la matriz nula). Suponemos, por tanto, que
f no es la forma idénticamente nula. Procedemos por inducción: para
n = 1, el resultado es siempre
cierto (...). Hipótesis de inducción: lo suponemos cierto para todos los espacios vectoriales de
dimensión
n - 1. Tomemos ahora
V de dimensión
n.
Afirmación: Existe un vector no isótropo. Supongamos, por contra, que todos los vectores son
isótropos. Por la construcción de la forma cuadrática asociada a una forma bilineal, se tiene que
f (
u,
v) =
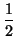
(
f (
u +
v,
u +
v) -
f (
u,
u) -
f (
v,
v)),
y si todos los vectores son isótropos, es que
f (
u,
v) = 0 para cualesquiera
u,
v, con lo que la forma es
nula. Por tanto, existe un vector no isótropo,
u.
Afirmación:
< u > 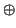 < u >
< u > 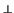 = V. Porque, al ser no isótropo, se tiene que
ker(f )
= V. Porque, al ser no isótropo, se tiene que
ker(f ) 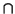 < u > = {0} y
< u >
< u > = {0} y
< u > 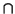 < u >
< u > 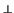 = {0}, de donde
< u >
= {0}, de donde
< u > 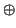 < u >
< u > 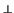 = V.
= V.
Fijamos el vector u y consideramos
W = < u > 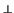 .
.
Seguimos. Tenemos ahora una forma bilineal simétrica en W, que es ni más ni menos que
f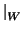 . Como
W tiene dimensión n - 1, aplicando la hipótesis de inducción sabemos que hay una base
. Como
W tiene dimensión n - 1, aplicando la hipótesis de inducción sabemos que hay una base
 W = {e2,..., en} ortogonal en W.
W = {e2,..., en} ortogonal en W.
Afirmación final: el conjunto
 = {u = e1,..., en} es una base ortogonal de V
para f. Lo único que hemos de probar es que es un sistema libre pues, por construcción, es un sistema
generador. Pero los ei son independientes para i > 1 y e1 = u no está en
W = < e2,..., en > por
construcción.
= {u = e1,..., en} es una base ortogonal de V
para f. Lo único que hemos de probar es que es un sistema libre pues, por construcción, es un sistema
generador. Pero los ei son independientes para i > 1 y e1 = u no está en
W = < e2,..., en > por
construcción.

Nota 1.3.4
El proceso es ``constructivo'': se procede por etapas. Primero se busca un vector que no esté en el núcleo
(a ojo de buen cubero, o bien,
f (
u,
u)
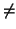
0). Una vez escogido, se construye el subespacio ortogonal a este
vector -que tiene dimensión
n - 1-. Se repite el proceso con
f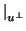
...
La expresión matricial del resultado anterior es:
PROPOSICIÓN 1.3.5
Toda forma bilineal simétrica admite una base para la cual su matriz es diagonal.
Demostración.
Tómese una base

= {
e1,...
en} ortogonal para
f. ¿Cómo es la matriz? Es, en
concreto,
M = (
Mij) donde
Mij =
f (
ei,
ej) y estos número son cero salvo para
i =
j:
con
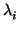
=
f (
ei,
ei). Si el ker(
f ) tiene dimensión
r, entonces las
r últimos lambdas
son 0, según la construcción de arriba.

.
Nota 1.3.6
Muy importante: el cambio de base que hemos hecho se traduce en matrices como
D =
PtMP (en hermíticas
como
D =
PtM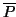
),
porque no es un endomorfismo, sino una forma bilineal.
COROLARIO 1.3.7
Una forma bilineal simétrica
no degenerada sobre
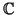
admite una base ortonormal.
Sobre

, toda forma bilineal
definida positiva admite una base ortonormal.
Demostración.
En
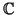
, se toma una base ortogonal

= (
e1,...,
en) y ahora se normaliza:


= (
e'1,...,
e'n) con
e'i =
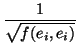 ei
ei
y terminamos. En

podemos hacer lo mismo sólo cuando
f (
ei,
ei) > 0, es decir, cuando
f
es definida positiva.

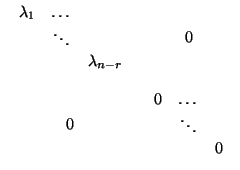
Nota 1.3.8 (Nota sobre el rango)
Si
dim(ker(
f )) =
r, entonces existen
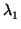
,...,
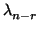
en
K y una
base

de V, tales que la matriz de
f en la base

es precisamente
ESTO LO EXPLIQUÉ OTRO DÍA
Nota 1.3.9
Un proceso que se puede seguir para construir el cambio de base de manera matricial, es el siguiente:
triangularizar la matriz ``por la derecha'', con operaciones elementales por columnas. Como es simétrica,
las mismas operaciones ``por la izquierda'' -esto es, por filas- diagonalizan.. Más gráficamente, se toma
la matriz siguiente:
y se triangulariza superiormente (se ponen 0 sobre la diagonal) la matriz de la izquierda mediante
operaciones por columnas, repitiendo la misma operación cada vez con las filas correspondientes. A la matriz
de la derecha (que es la identidad, al principio) se le aplican las mismas transformaciones
pero sólo
por columnas. Una vez terminado el proceso, la matriz de la derecha es
P.
Pega: si en un momento del
proceso aparece un 0 en la diagonal que nos impide seguir triangularizando, hay que hacer lo
siguiente. Escogemos una columna que tenga, al mismo nivel, un elemento no nulo. Sumamos ésta a la del 0
(y, por tanto, hacemos la misma operación en la matriz de la derecha). Ahora
hemos de hacer en M (la
izquierda) la misma operación por filas y no hacer nada a la derecha.
Ejemplo: calcúlese una base ortogonal para la forma bilineal
f :  3×
3× 3
3 
 que, en la base canónica tiene por matriz la siguiente:
Procedimiento: escribimos la matriz y a su lado, la identidad:
Paso 1: ``simplificamos la primera fila''. Para ello hemos de restar a la segunda columna el doble
de la primera y a la tercera columna el triple de la primera:
Paso 1-por filas: repetimos la operación por filas, sólo en la matriz de la izquierda:
Paso 2: El 0 de la posición 2, 2 nos impide seguir la triangulación, pues tenemos el -1 del
lugar 3, 2. Sumamos a la segunda columna, la tercera en ambas matrices:
Paso 2-por filas: Repetimos la operación con las filas (2 y 3) en la matriz de la
izquierda. Esto es, sumamos a la segunda fila, la tercera:
Paso 3: continuamos con la diagonalización ``como si no hubiera pasado nada''. Hemos de restar a
la tercera columna la segunda multiplicada por 4/5:
Paso 3-por filas: como siempre, en la matriz de la derecha no tocamos nada.
Hemos terminado. El cambio dado por la matriz
o, lo que es lo mismo, la base
convierten la forma bilineal de partida en
que, en la base canónica tiene por matriz la siguiente:
Procedimiento: escribimos la matriz y a su lado, la identidad:
Paso 1: ``simplificamos la primera fila''. Para ello hemos de restar a la segunda columna el doble
de la primera y a la tercera columna el triple de la primera:
Paso 1-por filas: repetimos la operación por filas, sólo en la matriz de la izquierda:
Paso 2: El 0 de la posición 2, 2 nos impide seguir la triangulación, pues tenemos el -1 del
lugar 3, 2. Sumamos a la segunda columna, la tercera en ambas matrices:
Paso 2-por filas: Repetimos la operación con las filas (2 y 3) en la matriz de la
izquierda. Esto es, sumamos a la segunda fila, la tercera:
Paso 3: continuamos con la diagonalización ``como si no hubiera pasado nada''. Hemos de restar a
la tercera columna la segunda multiplicada por 4/5:
Paso 3-por filas: como siempre, en la matriz de la derecha no tocamos nada.
Hemos terminado. El cambio dado por la matriz
o, lo que es lo mismo, la base
convierten la forma bilineal de partida en
HASTA AQUÍ LO QUE EXPLIQUÉ UN DÍA APARTE



Next: Clasificación de las formas
Up: FORMAS BILINEALES
Previous: Propiedades del ortogonal.
Pedro Fortuny Ayuso
2001-06-15
![]() K.
K.
![]() < u >
< u > ![]() = V. Porque, al ser no isótropo, se tiene que
ker(f )
= V. Porque, al ser no isótropo, se tiene que
ker(f ) ![]() < u > = {0} y
< u >
< u > = {0} y
< u > ![]() < u >
< u > ![]() = {0}, de donde
< u >
= {0}, de donde
< u > ![]() < u >
< u > ![]() = V.
= V.
![]() .
.
![]() . Como
W tiene dimensión n - 1, aplicando la hipótesis de inducción sabemos que hay una base
. Como
W tiene dimensión n - 1, aplicando la hipótesis de inducción sabemos que hay una base
![]() W = {e2,..., en} ortogonal en W.
W = {e2,..., en} ortogonal en W.
![]() = {u = e1,..., en} es una base ortogonal de V
para f. Lo único que hemos de probar es que es un sistema libre pues, por construcción, es un sistema
generador. Pero los ei son independientes para i > 1 y e1 = u no está en
W = < e2,..., en > por
construcción.
= {u = e1,..., en} es una base ortogonal de V
para f. Lo único que hemos de probar es que es un sistema libre pues, por construcción, es un sistema
generador. Pero los ei son independientes para i > 1 y e1 = u no está en
W = < e2,..., en > por
construcción.
![]()