- a)
-
(L1
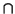 L2)
L2)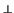
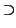 L1
L1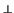 + L2
+ L2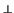 .
.
- b)
-
(L1 + L2)
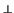 = L1
= L1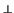
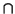 L2
L2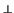 .
.
- c)
-
(L
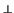 )
)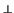
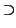 L.
L.
Enumeramos (y ``demostramos'') a continuación las propiedades básicas de los subconjuntos ortogonales.
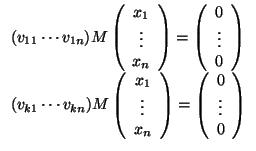
Un ejemplo de que pueden no ser iguales es
V = ![]() 3 y f una forma bilineal simétrica de matriz
(en una base
(e1, e2, e3)):
3 y f una forma bilineal simétrica de matriz
(en una base
(e1, e2, e3)):
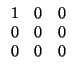
La inclusión recíproca se demuestra del siguiente modo: sabemos, por la propiedad 2), que
L1![]()
![]() (L1 + L2)
(L1 + L2)![]() y, por el mismo precio,
L2
y, por el mismo precio,
L2![]()
![]() (L1 + L2)
(L1 + L2)![]() . Por tanto,
L1
. Por tanto,
L1![]()
![]() L2
L2![]()
![]() (L1 + L2)
(L1 + L2)![]() .
.
![$\displaystyle \begin{array}{l}
\dim (L) + \dim(L^{\perp})\dim(V) \\ [1ex] \dim (L^{\perp})+\dim ((L^{\perp})^{\perp})=\dim V
\end{array}$](img101.gif)
Para demostrar que en a) también hay igualdad en el caso no degenerado, se hace un razonamiento algo artificial: por una parte, como hemos demostrado c) en este caso y como b) es siempre cierto, se tiene
| ((L1 |
| (L1 |