


Next: Ecuaciones de subespacios afines
Up: El espacio afín
Previous: Referencia en un espacio
Fijemos un espacio afín
(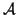 , V) de dimensión n sobre un cuerpo K. Vamos a hacer un poco
de geometría de puntos, rectas, planos, hiperplanos afines, es decir, formados por puntos ``de
verdad'', no por vectores.
, V) de dimensión n sobre un cuerpo K. Vamos a hacer un poco
de geometría de puntos, rectas, planos, hiperplanos afines, es decir, formados por puntos ``de
verdad'', no por vectores.
Definición 2.1.3
Un
subespacio del espacio afín

es un subconjunto
S 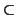

tal que el
conjunto de vectores
es un subespacio vectorial de
V.
Nota 2.1.4
El conjunto vacío se toma como subespacio afín (i. e. como espacio).
Definición 2.1.5
Sea



un punto del espacio afín y
E 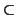 V
V un subespacio vectorial de
V. Llamamos
subespacio afín que pasa por  y tiene la dirección de E
y tiene la dirección de E al conjunto
formado por los puntos

+
v, donde
v ``recorre'' los vectores de
E:
S(

,
E) = {
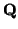
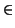
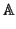
: hay un
v 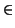 E
E con
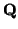
=

+
v}.
Nota 2.1.6
Nótese que el par
(
S(

,
E),
E) es un espacio afín según la definición que dimos arriba.
Con la notación de la definición, E se llama variedad de dirección de
S( , E). Si nos dan
un conjunto
S
, E). Si nos dan
un conjunto
S 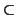
 que es un subespacio afín de
que es un subespacio afín de
 , entonces (por ser
subespacio), la familia de vectores
L = {
, entonces (por ser
subespacio), la familia de vectores
L = {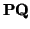 :
:  ,
,
 S} es un subespacio vectorial de
V. Es elemental comprobar que, dado cualquier punto
S} es un subespacio vectorial de
V. Es elemental comprobar que, dado cualquier punto
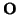
 S, se tiene la igualdad
S = S(
S, se tiene la igualdad
S = S(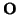 , L). Esto se suele decir ``la variedad de direcciones de un subespacio afín está determinada por el
subespacio''.
, L). Esto se suele decir ``la variedad de direcciones de un subespacio afín está determinada por el
subespacio''.
HASTA AQUÍ CLASE 8: 990302
LEMA 2.1.7
Sea
(

,
V) un espacio afín y
S = (

,
E),
S' = (
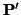
,
E') dos subespacios afines. Se da
la igualdad
S =
S' si y sólo si
E =
E' y además
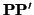
 E
E.
Demostración.
Por simetría, basta que demostremos una de las dos inclusiones. Veamos que
S 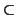 S'
S'. Sea

un punto de
S. Sabemos que
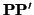
 E
E y como
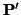
 S'
S', entonces

 S'
S'. Así
pues, al ser
E =
E', cualquier punto de

de la forma

+
e, con
e  E
E, está en
S'. Pero

=

+
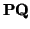
. Por tanto,

 S'
S'.

Definición 2.1.8
La
dimensión de un espacio afín
(

,
V) es la dimensión de
V, salvo cuando

es vacío, en cuyo caso
dim(

) = - 1.
PROPOSICIÓN 2.1.9
Dada una familia cualquiera
{
Si =
S(
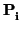
,
Ei)}
i 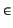 I
I de subespacios afines de un espacio
afín
(

,
V), el conjunto intersección
S =
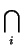 Si
Si
es un subespacio afín de

(que puede ser vacío).
Demostración.
Si la intersección es vacía, automáticamente es un subespacio afín. Supongamos, pues que no es
vacía. Basta con que demostremos que existe un punto



y un subespacio vectorial
E de
V tales que
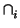 Si
Si =
S(

,
E). Fijamos un punto cualquiera

 S
S =
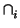 Si
Si. Tomemos el subconjunto de
V siguiente:
es decir, el conjunto formado por todos los vectores que parten de

y llegan a otro punto de la
intersección. Si demostramos que
E es un subespacio vectorial hemos terminado, pues automáticamente ha
de ser
S =
S(

,
E).
Sean, pues u, v  E y
E y
 ,
,
 K. Consideremos el vector
w =
K. Consideremos el vector
w =  u +
u +  v. Como u, v
v. Como u, v  E,
existen
E,
existen
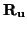 y
y
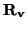 en S tales que
u =
en S tales que
u = 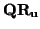 , v =
, v = 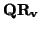 . Al estar
. Al estar
 ,
,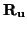 y
y
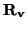 en todos los Si, también lo están
en todos los Si, también lo están
 =
=  +
+  u y
u y
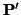 =
=  +
+  v =
v =  +
+  u +
u +  v, que es lo que queríamos comprobar.
v, que es lo que queríamos comprobar.

Operaciones con subespacios afines. En la proposición anterior hemos demostrado que la intersección
de subespacios afines es un subespacio afín. Vamos ahora a construir el subespacio ``suma'' y el
``linearizado'' de un subconjunto de puntos.
Definición 2.1.10
Dado un subconjunto
S 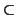

de un espacio afín, definimos el
linearizado de S, que
denotaremos
LA(
S), (
A de afín) como el menor subespacio afín de

que contiene a
S. Dada una familia
(
Si,
Ei) de subespacios afines de

, se define el
subespacio
suma
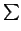 (Si, Ei)
(Si, Ei) como el linearizado de la unión
S =
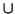 Si
Si (el menor subespacio afín que
contiene a todos los
Si).
Definición 2.1.11
Sean
S1 y
S2 dos subconjuntos de un espacio afín
(

,
V). Se dice que
S2 depende afínmente de S1, si
S2 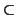 LA
LA(
S1). Se comprueba de modo elemental que
- a)
- S1 depende afínmente de S1.
- b)
- Si
S1
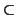 S2, entonces S1 depende afínmente de S2.
S2, entonces S1 depende afínmente de S2.
- c)
- Si S1 depende afínmente de S2 y S2 depende afínmente de S3, entonces
S1 depende afínmente de S3.
En particular, se dice que un punto

depende afínmente de los puntos
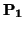
,...,
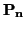
si
{

} depende afínmente de
{
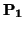
,...,
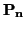
}.
PROPOSICIÓN 2.1.12
Si
S 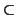

es un subconjunto de

y

 S
S es un punto cualquiera de
S,
entonces el linearizado de
S es
LA(
S) = (

,
E), donde
E =
L({
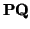
:

 S
S}). Es decir,
para calcular el linearizado no hay más que conocer un punto
P y calcular el linearizado del conjunto de
``vectores que puedo formar en
S partiendo de

''.
Demostración.
Que la construcción de
LA(
S) de arriba es un subespacio afín es evidente (punto + variedad de
direcciones). Que es el más pequeño es también evidente, pues la variedad de direcciones de cualquier
subespacio afín que contenga a
S debe contener todos los vectores
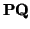
con

 S
S, y por
tanto, debe contener a
E.

COROLARIO 2.1.13
Si
(
Si)
i 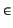 I
I es una familia de subespacios de un espacio afín
(

,
V), donde
Si =
S(
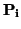
,
Ei), entonces
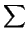 Si
Si =
S(

,
E)
con

=
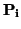
para un
i cualquiera y
E =
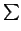 Ei
Ei +
L({
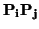
:
j  I
I}).
Demostración.
Se deja como ejercicio que conviene hacer.

Hay que tener en la cabeza tanto los Ei como los
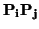 : en el espacio afín
: en el espacio afín
 3, la suma de dos rectas que se cruzan es el total, mientras que la suma de dos rectas que se cortan en
un punto es un plano.
3, la suma de dos rectas que se cruzan es el total, mientras que la suma de dos rectas que se cortan en
un punto es un plano.
También se deja como ejercicio la comprobación del siguiente resultado importante (a la hora de hacer
cuentas):
COROLARIO 2.1.14
Sean
S1 =
S(
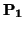
,
E1) y
S2 = (
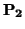
,
E2) dos subespacios afines de un espacio afín
(

,
V). Se tiene
- Si
S1
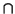 S2
S2 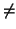
 entonces
S1 + S2 = S(
entonces
S1 + S2 = S(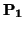 , E1 + E2).
, E1 + E2).
- Si
S1
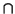 S2 =
S2 = 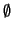 entonces
S1 + S2 = S(
entonces
S1 + S2 = S(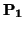 , E1 + E2 + L(
, E1 + E2 + L(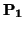
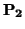 )).
)).
TEOREMA 2.1.15 (Fórmula afín de las dimensiones)
Sean
S1 y
S2 dos subespacios afines de un espacio afín
(

,
V). Se verifica siempre
que
dim(
S1) + dim(
S2)
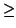
dim(
S1 +
S2) + dim(
S1 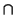 S2
S2).
Y se tiene la igualdad sólo en los dos casos siguientes:
- a)
- Cuando
S1
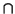 S2
S2 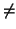
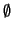 .
.
- b)
- Cuando
S1
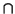 S2 =
S2 = 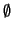 y la intersección de las variedades de dirección de S1 y
S2 es exactamente {0}.
y la intersección de las variedades de dirección de S1 y
S2 es exactamente {0}.
Demostración.
Escribimos
S1 =
S(
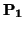
,
E1) y
S2 =
S(
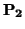
,
E2). Vamos a distinguir dos casos.
-
S1
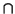 S2
S2 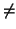
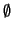 . Entonces
S1 + S2 = S(
. Entonces
S1 + S2 = S(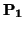 , E1 + E2), según el Corolario
1.14. También se tiene que si
, E1 + E2), según el Corolario
1.14. También se tiene que si

 S1
S1 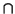 S2, entonces
S1
S2, entonces
S1 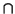 S2 = S(
S2 = S( , E1
, E1 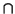 E2). Por tanto,
E2). Por tanto,
dim(
S1 +
S2) + dim(
S1 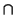 S2
S2) = dim(
E1 +
E2) + dim(
E1 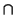 E2
E2) =
= dim(
E1) + dim(
E2) = dim(
S1) + dim(
S2)
por definición. Con lo que se tiene la fórmula.
- Cuando
S1
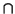 S2 =
S2 = 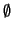 , el vector
, el vector
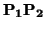 no está en
E1 + E2. (Se deja
como ejercicio comprobar eso). Por tanto,
no está en
E1 + E2. (Se deja
como ejercicio comprobar eso). Por tanto,
| |
dim(E1 + E2 + L(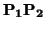 )) = )) = |
|
| |
= dim(E1 + E2) + dim(L(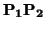 )) - dim((E1 + E2) )) - dim((E1 + E2) 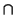 L( L(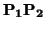 )) = )) = |
|
| |
= dim(E1 + E2) + 1 - 0 = dim(E1 + E2) + 1. |
|
y, por tanto,
| |
dim(S1 + S2) + dim(S1 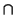 S2) = S2) = |
|
| |
= dim(E1 + E2) + 1 - 1 = dim(E1 + E2) = |
|
| |
= dim(E1) + dim(E2) - dim(E1 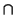 E2) = E2) = |
|
| |
= dim(S1) + dim(S2) - dim(E1 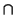 E2) E2) |
|
de donde
dim(
S1 +
S2) + dim(
S1 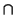 S2
S2)
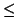
dim(
S1) + dim(
S2)
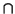 E2 = {0}.
E2 = {0}.

Definición 2.1.16
Dos subespacios afines
S1 = (
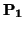
,
E1) y
S2 = (
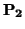
,
E2)
se cortan si su
intersección es no vacía. Diremos que
se cruzan si su intersección es vacía
y
además,
E1 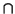 E2
E2 = {0}. Son
paralelos si
E1 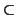 E2
E2 (ó
E2 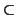 E1
E1) y
son
estrictamente paralelos si son paralelos y no se cortan. La igualdad en la fórmula de las
dimensiones se verifica si y sólo si
S1 y
S2 se cortan o se cruzan y no se verifica si y sólo si
son estrictamente paralelos.
HASTA AQUÍ CLASE 9: 990304



Next: Ecuaciones de subespacios afines
Up: El espacio afín
Previous: Referencia en un espacio
Pedro Fortuny Ayuso
2001-06-15
![]() , V) de dimensión n sobre un cuerpo K. Vamos a hacer un poco
de geometría de puntos, rectas, planos, hiperplanos afines, es decir, formados por puntos ``de
verdad'', no por vectores.
, V) de dimensión n sobre un cuerpo K. Vamos a hacer un poco
de geometría de puntos, rectas, planos, hiperplanos afines, es decir, formados por puntos ``de
verdad'', no por vectores.
![]() E y
E y
![]() ,
,![]()
![]() K. Consideremos el vector
w =
K. Consideremos el vector
w = ![]() u +
u + ![]() v. Como u, v
v. Como u, v ![]() E,
existen
E,
existen
![]() y
y
![]() en S tales que
u =
en S tales que
u = ![]() , v =
, v = ![]() . Al estar
. Al estar
![]() ,
,![]() y
y
![]() en todos los Si, también lo están
en todos los Si, también lo están
![]() =
= ![]() +
+ ![]() u y
u y
![]() =
= ![]() +
+ ![]() v =
v = ![]() +
+ ![]() u +
u + ![]() v, que es lo que queríamos comprobar.
v, que es lo que queríamos comprobar.
![]()