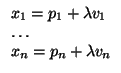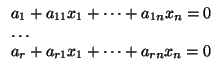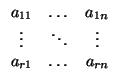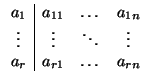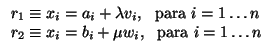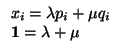Next: Ecuaciones de un hiperplano.
Up: El espacio afín
Previous: Ecuaciones de subespacios afines
Como antes,
( , V) es un espacio afín de dimensión n.
, V) es un espacio afín de dimensión n.
Una recta es (...) un subespacio afín de dimensión 1. La demostración del siguiente resultado
es un ejercicio teórico muy sencillo:
PROPOSICIÓN 2.1.18
Dados dos puntos distintos

,

en un espacio afín

, existe una única recta
que los contiene.
Estudiemos las rectas por medio de coordenadas. Sea
 = (
= (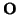 ,(e1,..., en)) una
referencia afín de
,(e1,..., en)) una
referencia afín de
 . Supongamos que los puntos
. Supongamos que los puntos  y
y  (que tomamos distintos)
tienen, respectivamente, coordenadas
(p1,..., pn) y
(q1,..., qn). Entonces la ecuación
paramétrica de
LA(
(que tomamos distintos)
tienen, respectivamente, coordenadas
(p1,..., pn) y
(q1,..., qn). Entonces la ecuación
paramétrica de
LA( ,
, ) es
) es
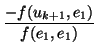
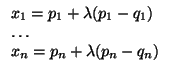 Atención: sólo hay un $&lambda#lambda;$.
Atención: sólo hay un $&lambda#lambda;$.
Si llamamos v al vector
v =  y lo escribimos en coordenadas
v = (v1,..., vn) (o si sólo nos
dan un punto
y lo escribimos en coordenadas
v = (v1,..., vn) (o si sólo nos
dan un punto  y un vector v), tenemos que las ecuaciones paramétricas de la recta que pasa
por
y un vector v), tenemos que las ecuaciones paramétricas de la recta que pasa
por  y tiene dirección v son
que eran conocidas por todos, supongo.
y tiene dirección v son
que eran conocidas por todos, supongo.
De todas las discusiones de este capítulo, se deduce que un sistema de r ecuaciones implícitas
define una recta afín en
 (recuerdo que
(recuerdo que
 tiene dimensión n) si y sólo si
Atención: hay que comprobar que el rango de la matriz (aij) es el mismo que el de la extendida
(si no, lo que definen esas ecuaciones es el conjunto vacío). Un ejemplo: las ecuaciones x + y = 0 y
x + y + 1 = 0 no definen una recta en
tiene dimensión n) si y sólo si
Atención: hay que comprobar que el rango de la matriz (aij) es el mismo que el de la extendida
(si no, lo que definen esas ecuaciones es el conjunto vacío). Un ejemplo: las ecuaciones x + y = 0 y
x + y + 1 = 0 no definen una recta en
 3 porque no se cortan.
3 porque no se cortan.
Dos rectas r1 y r2 son paralelas cuando sus variedades de dirección son la misma. Si las
tenemos expresadas en paramétricas:
entonces son paralelas si y sólo si los vectores
v = (v1,..., vn) y
v = (w1,..., wn) son
linealmente dependientes. (Si las rectas son la misma, entonces también son paralelas, ojo). Son
estrictamente paralelas si además de ser paralelas, su intersección es vacía, es decir, si los
vectores
(a1 - b1,..., an - bn) y
v = (v1,..., vn) son independientes. (Donde ponemos v
podemos poner w, puesto que estos dos son proporcionales por ser paralelas).
Para terminar, las dos rectas r1 y r2 de arriba se cruzan si y sólo si no se cortan y los vectores
v y w son linealmente independientes. Esto se resume en que los tres vectores
(a1 - b1,..., an - bn), v, w son linealmente independientes. Dejamos los detalles como ejercicio
facilísimo.
En cualquier otro caso, se cortan en un sólo punto.
ATENCIÓN
Otra vez, en el Aroca, os encontráis las ecuaciones
pero mejor no liarse



Next: Ecuaciones de un hiperplano.
Up: El espacio afín
Previous: Ecuaciones de subespacios afines
Pedro Fortuny Ayuso
2001-06-15
![]() , V) es un espacio afín de dimensión n.
, V) es un espacio afín de dimensión n.
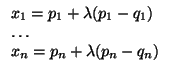 Atención: sólo hay un $&lambda#lambda;$.
Atención: sólo hay un $&lambda#lambda;$.