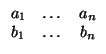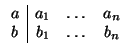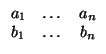Next: El plano afín
Up: El espacio afín
Previous: Ecuaciones de una recta.
Definición 2.1.19
Un
hiperplano de un espacio afín
(

,
V) de dimensión
n es un subespacio afín de
dimensión
n - 1.
Utilizaremos la misma referencia
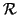 = (
= (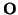 ,(e1,..., en)) de la sección anterior. De la
definición se deduce que un subespacio afín se puede definir mediante:
,(e1,..., en)) de la sección anterior. De la
definición se deduce que un subespacio afín se puede definir mediante:
- Un punto
 y n - 1 vectores linealmente independientes. En este caso, si las coordenadas de
y n - 1 vectores linealmente independientes. En este caso, si las coordenadas de
 son
son
 = (p1,..., pn) y los vectores
v1,..., vn-1 linealmente independientes se
escriben
vi = (vi1,..., vin), para
i = 1...n - 1, entonces el hiperplano que pasa por
= (p1,..., pn) y los vectores
v1,..., vn-1 linealmente independientes se
escriben
vi = (vi1,..., vin), para
i = 1...n - 1, entonces el hiperplano que pasa por  y
cuya variedad de dirección está generada por
v1,..., vn tiene coordenadas paramétricas
y
cuya variedad de dirección está generada por
v1,..., vn tiene coordenadas paramétricas
- n puntos afínmente independientes. Es decir, n puntos
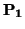 ,...,
,...,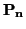 tales que
los vectores
tales que
los vectores
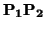 ,...,
,...,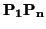 son linealmente independientes. Si estos puntos tienen
por coordenadas
son linealmente independientes. Si estos puntos tienen
por coordenadas
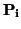 = (pi1,..., pin), entonces las ecuaciones paramétricas del plano que pasa
por ellos son
= (pi1,..., pin), entonces las ecuaciones paramétricas del plano que pasa
por ellos son
De todo esto se deduce también que un hiperplano queda determinado por una sola ecuación implícita
b + x1a1 + ... + xnan = 0,
donde se supone que no todos los ai son nulos, claro.
Paralelismo de hiperplanos. Dos hiperplanos
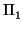 ,
,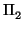 son paralelos si sus variedades de
dirección son la misma. Si las ecuaciones implícitas de
son paralelos si sus variedades de
dirección son la misma. Si las ecuaciones implícitas de 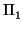 y
y 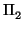 son, respectivamente
son, respectivamente
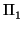 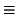 a + x1a1 + ... + xnan = 0 a + x1a1 + ... + xnan = 0 |
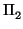 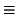 b + x1b1 + ... + xnbn = 0 b + x1b1 + ... + xnbn = 0 |
entonces sus variedades de dirección son, respectivamente
x1a1 + ... + xnan = 0 y
x1b1 + ... + xnbn = 0, y éstas coinciden si y sólo si los vectores
(a1,..., an) y
(b1,..., bn) son linealmente dependientes (i. e. proporcionales). Para que sean estrictamente
paralelos se tiene que cumplir también que los vectores
(a1,..., an, a) y
(b1,..., bn, b)
sean linealmente independientes. En términos matriciales:
mientras que
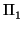
y
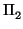
estrictamente paralelos
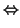
paralelos y rg
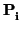
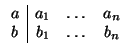
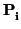
= 2
Atención: Para saber si son estrictamente paralelos hay que comprobar que son paralelos, es decir,
que el rango de la matriz
es 1. No vale con decir que el rango de la extendida es 2, pues eso también lo cumplen hiperplanos que
se cortan.



Next: El plano afín
Up: El espacio afín
Previous: Ecuaciones de una recta.
Pedro Fortuny Ayuso
2001-06-15
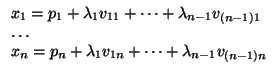
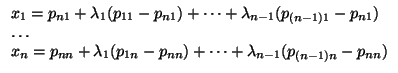
![]() ,
,![]() son paralelos si sus variedades de
dirección son la misma. Si las ecuaciones implícitas de
son paralelos si sus variedades de
dirección son la misma. Si las ecuaciones implícitas de ![]() y
y ![]() son, respectivamente
son, respectivamente