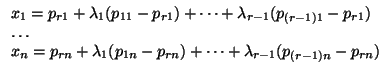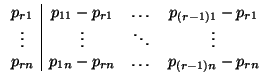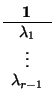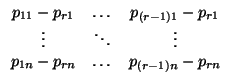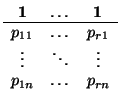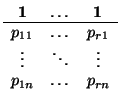Next: Ecuaciones de una recta.
Up: El espacio afín
Previous: Subespacios de un espacio
Fijamos un espacio afín
( , V) de dimensión n sobre el cuerpo K. Puesto que vamos a
hablar de ecuaciones, lo primero que necesitamos es un sistema de coordenadas. En los espacios afines, las
coordenadas se dan relativas a una referencia. Por tanto, suponemos que tenemos una referencia
, V) de dimensión n sobre el cuerpo K. Puesto que vamos a
hablar de ecuaciones, lo primero que necesitamos es un sistema de coordenadas. En los espacios afines, las
coordenadas se dan relativas a una referencia. Por tanto, suponemos que tenemos una referencia
 = (
= ( ,(e1,..., en)).
,(e1,..., en)).
I.-Ecuaciones paramétricas de un subespacio
S( , E).
, E).
Sea


 y E un subespacio vectorial de V. Pretendemos estudiar las coordenadas del
subespacio de
y E un subespacio vectorial de V. Pretendemos estudiar las coordenadas del
subespacio de
 que pasa por
que pasa por  y tiene por variedad de dirección a E, es decir, de
S(
y tiene por variedad de dirección a E, es decir, de
S( , E). El subespacio vectorial E tendrá unas coordenadas paramétricas
, E). El subespacio vectorial E tendrá unas coordenadas paramétricas
como subespacio de V, donde la matriz (vij) es la matriz de un sistema de generadores
(v1,..., vr) de E escrito en la base
(e1,..., en). El punto  tendrá unas
coordenadas
(p1,..., pn) en la referencia
tendrá unas
coordenadas
(p1,..., pn) en la referencia
 . Si
. Si  es otro punto de
es otro punto de
 con coordenadas
(q1,..., qn), se tiene que
con coordenadas
(q1,..., qn), se tiene que

 S(
S( , E) si y sólo si
, E) si y sólo si
 =
=  + v con v
+ v con v  E. Es decir,
(q1,..., qn)
E. Es decir,
(q1,..., qn)  S(
S( , E) si y sólo si existen
, E) si y sólo si existen
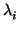
 K
con
K
con
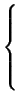 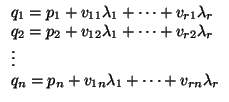 |
(2.1) |
que, matricialmente se expresa: un punto
(x1,..., xn) está en
S( , E) si y sólo si
De toda esta construcción se deduce que
, E) si y sólo si
De toda esta construcción se deduce que
- La matriz de términos independientes es la matriz (vector) de coordenadas de un punto de
S(
 , E) que no es necesariamente
, E) que no es necesariamente  .
.
- Los vectores
(e1,..., er) no tienen por qué ser independientes. En concreto,
dim(
S(

,
E)) = dim(
E) = rg
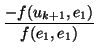
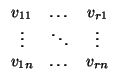
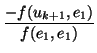
- Cualquier sistema de ecuaciones parámetricas como (2) define un subespacio
afín. Además, dado un sistema de ese tipo, se calcula el subespacio que describen
S = S(
 , E)
tomando como punto
, E)
tomando como punto  el dado por los términos independientes
(p1,..., pn) y como variedad
de direcciones el subespacio vectorial de V generado por los vectores
(v11,..., v1n),...,(vr1,..., vrn).
el dado por los términos independientes
(p1,..., pn) y como variedad
de direcciones el subespacio vectorial de V generado por los vectores
(v11,..., v1n),...,(vr1,..., vrn).
II.-Ecuaciones implícitas de
S( , E).
, E).
Como antes, fijamos un punto


 con coordenadas
(p1,..., pn) en la referencia
con coordenadas
(p1,..., pn) en la referencia
 y un subespacio vectorial E de V. Supongamos que E está descrito en forma
implícita por las ecuaciones
y un subespacio vectorial E de V. Supongamos que E está descrito en forma
implícita por las ecuaciones
que significa que un vector
(x1,..., xn) pertenece a E si y sólo si
Un punto


 estará en
S(
estará en
S( , E) si y sólo si el vector
, E) si y sólo si el vector 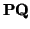 está en
E. En coordenadas, si
está en
E. En coordenadas, si
 = (p1,..., pn) y
= (p1,..., pn) y
 = (q1,..., qn) entonces
= (q1,..., qn) entonces

 S(
S( , E) si y sólo si
, E) si y sólo si
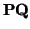
= (
q1 -
p1,...,
qn -
pn)
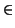 E
E
es decir, si y sólo si
o, lo que es lo mismo, escribiéndolo en forma de ecuación (en las incógnitas qi):
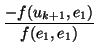 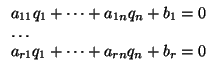 |
(2.2) |
donde
bi = - ai1p1 - ... - ainpn se obtiene haciendo el producto
Y se tienen los siguientes resultados:
- Cualquier sistema de la forma (3) define una subvariedad afín de
 (que puede ser el vacío si el sistema no tiene solución).
(que puede ser el vacío si el sistema no tiene solución).
- Dado un sistema de la forma (3), si llamamos S a la variedad afín que
define, entonces
S = S(
 , E), donde
, E), donde
 = (p1,..., pn) es una solución particular del
sistema (3) y E es el subespacio de V definido por el sistema
que es el sistema homogéneo asociado a (3).
= (p1,..., pn) es una solución particular del
sistema (3) y E es el subespacio de V definido por el sistema
que es el sistema homogéneo asociado a (3).
- La dimensión de S es la de L, que es
n - rg(aij) siempre que el sistema
(3) tenga solución. Si no la tiene, entonces
S =
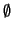 y
dim(S) = - 1. Esto
último ocurre cuando la matriz de coeficientes de (3) tiene rango menor que la
extendida.
y
dim(S) = - 1. Esto
último ocurre cuando la matriz de coeficientes de (3) tiene rango menor que la
extendida.
HASTA AQUÍ CLASE 10: 990305
III.-Ecuaciones del subespacio afín que pasa por r puntos.
Recordemos que hemos fijado una referencia
 = (
= ( ,(e1,..., en)) en el espacio
afín
,(e1,..., en)) en el espacio
afín
 . Vamos a escribir las ecuaciones parámetricas del subespacio ``generado'' por
r puntos. Es decir, del menor subespacio que los contiene. Llamemos
. Vamos a escribir las ecuaciones parámetricas del subespacio ``generado'' por
r puntos. Es decir, del menor subespacio que los contiene. Llamemos
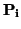 , con
i = 1...r a los
puntos de partida y escribamos en la referencia
, con
i = 1...r a los
puntos de partida y escribamos en la referencia
 sus coordenadas:
sus coordenadas:
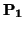 = (p11,..., p1n), ...,
= (p11,..., p1n), ...,
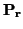 = (pr1,..., prn). Lo primero que hacemos es
calcular las ecuaciones paramétricas de la variedad de direcciones de
S = LA({
= (pr1,..., prn). Lo primero que hacemos es
calcular las ecuaciones paramétricas de la variedad de direcciones de
S = LA({ ,...,
,...,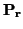 }), que llamaremos E. Como se vio arriba, E está generado por los vectores
{
}), que llamaremos E. Como se vio arriba, E está generado por los vectores
{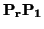 ,...,
,...,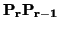 }. Es decir, un sistema de generadores
(v1,..., vr) de E
escrito en la base
(e1,..., en) es
}. Es decir, un sistema de generadores
(v1,..., vr) de E
escrito en la base
(e1,..., en) es
v1 = (p11 - pr1,..., p1n - prn),..., vr = (p(r-1)1 - pr1,..., p(r-1)n - prn)
y, por tanto, unas ecuaciones parámetricas de S son las siguientes:
(
x1,...,
xn)
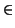 S
S 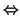
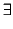
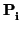
,...,
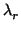
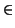 K
K con
ATENCIÓN
Nota 2.1.17
En el libro de Aroca (y es posible que en otros también) se encuentra la siguiente ecuación
``pseudoparamétrica'':
(
x1,...,
xn)
 S
S si y sólo si
pero prefiero no utilizarla porque lleva a confusión (uno piensa que tiene
r parámetros,
cuando en realidad como mucho tiene
r - 1).



Next: Ecuaciones de una recta.
Up: El espacio afín
Previous: Subespacios de un espacio
Pedro Fortuny Ayuso
2001-06-15
![]() , E).
, E).
![]()
![]()
![]() y E un subespacio vectorial de V. Pretendemos estudiar las coordenadas del
subespacio de
y E un subespacio vectorial de V. Pretendemos estudiar las coordenadas del
subespacio de
![]() que pasa por
que pasa por ![]() y tiene por variedad de dirección a E, es decir, de
S(
y tiene por variedad de dirección a E, es decir, de
S(![]() , E). El subespacio vectorial E tendrá unas coordenadas paramétricas
, E). El subespacio vectorial E tendrá unas coordenadas paramétricas
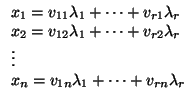
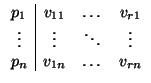
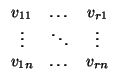
![]() , E).
, E).
![]()
![]()
![]() con coordenadas
(p1,..., pn) en la referencia
con coordenadas
(p1,..., pn) en la referencia
![]() y un subespacio vectorial E de V. Supongamos que E está descrito en forma
implícita por las ecuaciones
y un subespacio vectorial E de V. Supongamos que E está descrito en forma
implícita por las ecuaciones
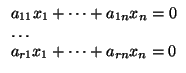
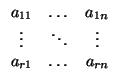
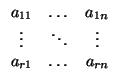
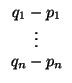
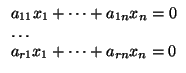
![]() = (
= (![]() ,(e1,..., en)) en el espacio
afín
,(e1,..., en)) en el espacio
afín
![]() . Vamos a escribir las ecuaciones parámetricas del subespacio ``generado'' por
r puntos. Es decir, del menor subespacio que los contiene. Llamemos
. Vamos a escribir las ecuaciones parámetricas del subespacio ``generado'' por
r puntos. Es decir, del menor subespacio que los contiene. Llamemos
![]() , con
i = 1...r a los
puntos de partida y escribamos en la referencia
, con
i = 1...r a los
puntos de partida y escribamos en la referencia
![]() sus coordenadas:
sus coordenadas:
![]() = (p11,..., p1n), ...,
= (p11,..., p1n), ...,
![]() = (pr1,..., prn). Lo primero que hacemos es
calcular las ecuaciones paramétricas de la variedad de direcciones de
S = LA({
= (pr1,..., prn). Lo primero que hacemos es
calcular las ecuaciones paramétricas de la variedad de direcciones de
S = LA({![]() ,...,
,...,![]() }), que llamaremos E. Como se vio arriba, E está generado por los vectores
{
}), que llamaremos E. Como se vio arriba, E está generado por los vectores
{![]() ,...,
,...,![]() }. Es decir, un sistema de generadores
(v1,..., vr) de E
escrito en la base
(e1,..., en) es
}. Es decir, un sistema de generadores
(v1,..., vr) de E
escrito en la base
(e1,..., en) es