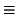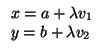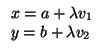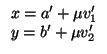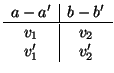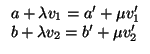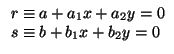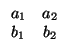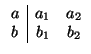Next: El espacio afín tridimensional
Up: ESPACIO AFÍN
Previous: Ecuaciones de un hiperplano.
Se llama plano afín sobre un cuerpo K al espacio afín de dimensión 2. Los únicos
subespacios afines del plano afín son, por tanto, el vacío, los puntos, las rectas y el
total. Además, las rectas son a la vez rectas e hiperplanos según la nomenclatura de la sección
anterior. Fijamos una referencia
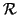 = (
= (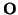 ,(e1, e2)). Utilizaremos coordenadas x, y.
,(e1, e2)). Utilizaremos coordenadas x, y.
I.- Una recta r en el plano afín viene determinada por
- Una ecuación paramétrica de la forma
donde (a, b) son las coordenadas de un punto de r y
(v1, v2) son las coordenadas del vector director
(que es un vector cualquiera que genere la variedad de direcciones de r).
- Una ecuación implícita:
a1x + a2y + a = 0
de la cual se puede extraer (a primera vista) la ecuación de la variedad de direcciones:
a1x + a2y = 0.
II.- Tomemos dos rectas r y s del plano, dadas por las ecuaciones paramétricas
Son paralelas si y sólo si los vectores
v = (v1, v2) y
v' = (v'1, v'2) son linealmente
dependientes. Son estrictamente paralelas si y sólo si ocurre eso y además
Si no son paralelas, es que se cortan. El punto de corte se encuentra solucionando el sistema (en las
variables 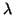 ,
, 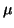 ):
que (si no son paralelas) tiene solución única. Una vez resuelto, se sustituye el
):
que (si no son paralelas) tiene solución única. Una vez resuelto, se sustituye el 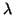 encontrado en
la ecuación de r y tenemos las coordenadas del punto.
encontrado en
la ecuación de r y tenemos las coordenadas del punto.
III.- Sean ahora r y s dos rectas cuyas ecuaciones implícitas conocemos:
Son paralelas si y sólo si
rg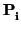
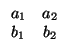
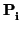 = 1. Son estrictamente paralelas si, además,
En cualquier otro caso, se cortan en un único punto (x, y), que es la solución del sistema formado por
las ecuaciones de las dos rectas.
= 1. Son estrictamente paralelas si, además,
En cualquier otro caso, se cortan en un único punto (x, y), que es la solución del sistema formado por
las ecuaciones de las dos rectas.
IV.- Si tenemos una recta
r 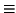 a + a1x + a2y = 0 dada en ecuaciones implícitas y otra
s
a + a1x + a2y = 0 dada en ecuaciones implícitas y otra
s 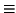 (x = p +
(x = p + 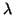 v1, y = q +
v1, y = q + 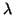 v2) dada en paramétricas, se tiene que:
v2) dada en paramétricas, se tiene que:
- a)
- Son paralelas si y sólo si
a1v1 + a2v2 = 0.
- b)
- Si no, se cortan en el punto determinado por el valor
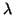 solución de la ecuación
solución de la ecuación
a +
a1(
p +
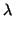 v1
v1) +
a2(
q +
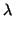 v2
v2) = 0.
V.- Haces de rectas. Dadas dos rectas en implícitas,
r 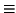 a + a1x + a2y = 0 y
s
a + a1x + a2y = 0 y
s 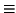 b + b1x + b2y = 0, definimos el haz de rectas generado por r y s como el conjunto de las rectas
r
b + b1x + b2y = 0, definimos el haz de rectas generado por r y s como el conjunto de las rectas
r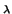 ,
,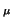 con ecuaciones
con ecuaciones
r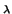 ,
,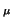
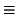
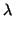
(
a +
a1x +
a2y) +
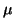
(
b +
b1x +
b2y) = 0.
- Si las rectas r y s se cortan en un punto P, entonces el haz de rectas generado por r y s es
exactamente el conjunto de las rectas que pasan por P.
- Si, por el contrario, las rectas son paralelas, entonces una recta está en el haz si y sólo si es
paralela a r (y, por tanto, a s), con lo que la ecuación de una recta cualquiera del haz es:
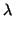
+
a1x +
a2y = 0.



Next: El espacio afín tridimensional
Up: ESPACIO AFÍN
Previous: Ecuaciones de un hiperplano.
Pedro Fortuny Ayuso
2001-06-15