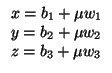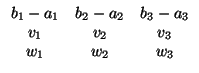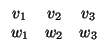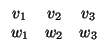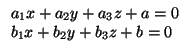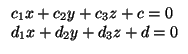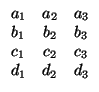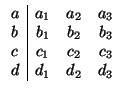Next: Coordenadas baricéntricas. Anexo.
Up: ESPACIO AFÍN
Previous: El plano afín
Se llama espacio afín tridimensional sobre un cuerpo K al espacio afín K3, con el espacio
vectorial subyacente K3 y la operación de ``suma de las coordenadas de un vector a las de un
punto''. Fijemos, como siempre, una referencia
 = (
= (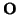 ,(e1, e2, e3)). Las coordenadas
de un punto genérico en esta referencia serán (x, y, z). Los subespacios afines son, como todo el mundo
sabe, el vacío, las rectas, los planos (dimensión 2) y el total. Los hiperplanos son los planos. Por
tanto, vienen determinados por una sóla ecuación afín.
,(e1, e2, e3)). Las coordenadas
de un punto genérico en esta referencia serán (x, y, z). Los subespacios afines son, como todo el mundo
sabe, el vacío, las rectas, los planos (dimensión 2) y el total. Los hiperplanos son los planos. Por
tanto, vienen determinados por una sóla ecuación afín.
I.- Sean 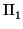 y
y 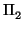 dos
planos de ecuaciones respectivas
dos
planos de ecuaciones respectivas
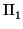
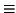 a + a1x + a2y + a3z = 0 y
a + a1x + a2y + a3z = 0 y
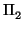
 b + b1x + b2y + b3z = 0. Para estudiar la relación entre ambos, ya vimos que hay que considerar las
matrices
b + b1x + b2y + b3z = 0. Para estudiar la relación entre ambos, ya vimos que hay que considerar las
matrices
Se pueden presentar, por tanto, tres casos
-
rg(M) = 2 (en cuyo caso coincide con
rg(
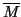 ). Los planos son distintos y no
son paralelos. Por tanto, se cortan en la recta cuyas ecuaciones implícitas son
Cualquier plano que contenga a esta recta tiene por ecuación una combinación lineal de las dos ecuaciones
de r. Se define el haz de planos de arista r como el conjunto de planos que contiene a r. Sus
elementos son los planos de la forma
). Los planos son distintos y no
son paralelos. Por tanto, se cortan en la recta cuyas ecuaciones implícitas son
Cualquier plano que contenga a esta recta tiene por ecuación una combinación lineal de las dos ecuaciones
de r. Se define el haz de planos de arista r como el conjunto de planos que contiene a r. Sus
elementos son los planos de la forma
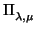 donde
donde
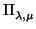
(
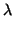 a
a +
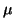 b
b) + (
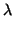 a1
a1 +
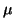 b1
b1)
x + (
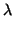 a2
a2 +
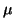 b2
b2)
y + (
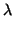 a3
a3 +
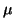 b3
b3)
z = 0
(se supone que  y
y  no son ambos 0, evidentemente).
no son ambos 0, evidentemente).
-
rg(M) = 1,
rg(
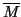 ) = 2. Los planos son paralelos y no se cortan, pues tienen la
misma variedad de direcciones (eso es que
rg(M) = 1) y no tienen puntos comunes. El haz de planos
paralelos a
) = 2. Los planos son paralelos y no se cortan, pues tienen la
misma variedad de direcciones (eso es que
rg(M) = 1) y no tienen puntos comunes. El haz de planos
paralelos a 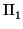 (y, por tanto, a
(y, por tanto, a 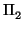 ) es el conjunto de planos
) es el conjunto de planos
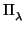 de la forma
(donde, como siempre, se supone
de la forma
(donde, como siempre, se supone

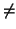 0).
0).
-
rg(M) = rg(
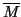 ) = 1. En este caso, los dos planos son iguales. El haz de planos
paralelos a ambos tiene la misma forma que en el caso anterior (claro).
) = 1. En este caso, los dos planos son iguales. El haz de planos
paralelos a ambos tiene la misma forma que en el caso anterior (claro).
II.- Tomemos dos rectas r, s cuyas ecuaciones paramétricas son
y llamemos
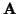 = (a1, a2, a3),
= (a1, a2, a3),
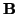 = (b1, b2, b3),
v = (v1, v2, v3) y
w = (w1, w2, w3). Hay dos posibilidades
= (b1, b2, b3),
v = (v1, v2, v3) y
w = (w1, w2, w3). Hay dos posibilidades
- Los vectores
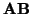 , v y w son linealmente independientes. En este caso, es claro que
r + s =
, v y w son linealmente independientes. En este caso, es claro que
r + s =  (todo el espacio) y de aquí concluimos que no se cortan y que, de hecho, se cruzan
(utilizando la fórmula de las dimensiones). Es evidente que si se cruzan, esos tres vectores han de ser
independientes. Por tanto, r y s se cruzan si y sólo si
(todo el espacio) y de aquí concluimos que no se cortan y que, de hecho, se cruzan
(utilizando la fórmula de las dimensiones). Es evidente que si se cruzan, esos tres vectores han de ser
independientes. Por tanto, r y s se cruzan si y sólo si
- Si los vectores
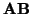 , v y w son linealmente dependientes, entonces el subespacio afín
generado por r y s tiene dimensión 2 como mucho. Ahora bien, puede ocurrir que v y w sean
linealmente independientes, en cuyo caso las rectas se cortan en un punto o que sean dependientes, y por
tanto, r y s son paralelas. Si son paralelas, entonces son estrictamente paralelas si
, v y w son linealmente dependientes, entonces el subespacio afín
generado por r y s tiene dimensión 2 como mucho. Ahora bien, puede ocurrir que v y w sean
linealmente independientes, en cuyo caso las rectas se cortan en un punto o que sean dependientes, y por
tanto, r y s son paralelas. Si son paralelas, entonces son estrictamente paralelas si 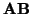 es
independiente de los otros dos. Es decir, suponiendo que el determinante de arriba es cero, entonces
es
independiente de los otros dos. Es decir, suponiendo que el determinante de arriba es cero, entonces
r y
s se cortan si y sólo si rg
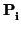
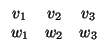
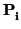
= 2
r y
s son paralelas si y sólo si rg
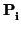
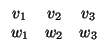
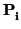
= 1
III.- Sean ahora r y s dos rectas cuyas ecuaciones implícitas conocemos:
y llamemos E al sistema formado por las cuatro ecuaciones que definen r y s. Pongamos ahora
Tenemos las siguientes posibilidades
-
rg(N) = 4. Por tanto,
rg(M) = 3 y las rectas se cruzan, pues tienen intersección
vacía y las variedades de dirección no son iguales.
-
rg(N) = 3 y
rg(M) = 3. En este caso el sistema E es compatible determinado y, por
tanto, las rectas se cortan en un sólo punto.
-
rg(N) = 3 y
rg(M) = 2. El sistema es incompatible. Por tanto, las rectas no se
cortan. Como las variedades de dirección tienen un vector común (y, al ser de dimensión 1, son
iguales), entonces r y s son estrictamente paralelas.
-
rg(N) = 2 y
rg(M) = 2. Las dos rectas son iguales.
Es decir, mediante el famoso teorema de Rouché (o con la fórmula de las dimensiones), podemos estudiar las
posiciones relativas de cualesquiera subespacios del espacio afín.
IV.- Dejamos la posición relativa de recta y plano como ejercicio elemental de C.O.U.



Next: Coordenadas baricéntricas. Anexo.
Up: ESPACIO AFÍN
Previous: El plano afín
Pedro Fortuny Ayuso
2001-06-15
![]() y
y ![]() dos
planos de ecuaciones respectivas
dos
planos de ecuaciones respectivas
![]()
![]() a + a1x + a2y + a3z = 0 y
a + a1x + a2y + a3z = 0 y
![]()
![]() b + b1x + b2y + b3z = 0. Para estudiar la relación entre ambos, ya vimos que hay que considerar las
matrices
b + b1x + b2y + b3z = 0. Para estudiar la relación entre ambos, ya vimos que hay que considerar las
matrices
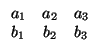
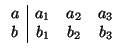
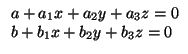
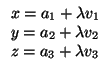 s
s