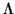Coordenadas baricéntricas. Anexo.

El baricentro de una familia finita de puntos es una noción física que responde al ``centro de masas'' de una familia de cuerpos adimensionales. ``Haciendo un paso al límite'' (integrales, etc...) se obtiene el concepto analítico de centro de masas de un sólido.

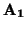
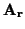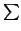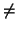
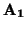
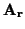
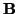
Definición 2.4.1   Sean $\bf A_{1}$,...,$\bf A_{r}$ r puntos de un espacio afín $\mathbb {A}$ de dimensión n sobre un cuerpo K. Fijemos, por otro lado, r números a₁,..., a_r $\in$ K, que llamaremos pesos de manera que $\sum$a_i $\neq$ 0. Se llama baricentro de la familia {$\bf A_{1}$,...,$\bf A_{r}$} con pesos a₁,..., a_r, a un punto $\bf B$ tal que existe $\bf O$ $\in$ $\mathbb {A}$ con

$$\bf OB$$ = $${\frac{{1}}{{\sum_{i=1}^{r} a_{i}}}}$$($$\sum_{{i=1}}^{{r}}$$a_i$$\bf OA_{i}$$).

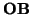
(Que quiere decir que el vector $\bf OB$ es ``la media ponderada de los $\bf OA_{i}$'').

En realidad, el punto $\bf O$ es irrelevante: si uno lo cumple, lo cumplen todos:

COROLARIO 2.4.2   Si $\bf O'$ es otro punto de $\mathbb {A}$ y $\bf B$ es el baricentro de {$\bf A_{1}$,...,$\bf A_{r}$} con pesos a₁,..., a_r, entonces

$$\bf O'B$$ = $${\frac{{1}}{{\sum_{i=1}^{r} a_{i}}}}$$($$\sum_{{i=1}}^{{r}}$$a_i$$\bf O'A_{i}$$).

Demostración. No hay más que considerar que $\bf O'A_{i}$ = $\bf O'O$ + $\bf OA_{i}$ y $\bf O'B$ = $\bf O'O$ + $\bf OB$; por tanto,

$$\bf O'B \bf O'O \bf OB \bf O'O {\frac{{1}}{{\sum_{i=1}^{r} a_{i}}}} \sum_{{i=1}}^{{r}} \bf OA_{i}$$

$$\bf O'O {\frac{{1}}{{\sum_{i=1}^{r} a_{i}}}} \sum_{{i=1}}^{{r}} \bf OO' \bf O'A_{i}$$

$$\bf O'O \bf OO' {\frac{{1}}{{\sum_{i=1}^{r} a_{i}}}} \sum_{{i=1}}^{{r}} \bf O'A_{i}$$

$${\frac{{1}}{{\sum_{i=1}^{r} a_{i}}}} \sum_{{i=1}}^{{r}} \bf O'A_{i}$$

$\qedsymbol$

Por tanto, tomando $\bf B$ = $\bf O$ en la definición, se tiene que

Definición 2.4.3 (Re-definición del baricentro)   El punto $\bf B$ es el baricentro de los puntos {$\bf A_{1}$,...,$\bf A_{r}$} con pesos a₁,..., a_r si y sólo si

$$\sum_{{i=1}}^{{r}}$$a_i$$\bf BA_{i}$$ = 0.

En general, si no se especifican pesos, se supone que son todos 1. Y por tanto, $\bf B$ es el baricentro de {$\bf A_{1}$,...,$\bf A_{r}$} si y sólo si $\sum$$\bf BA_{i}$ = 0. Si r = 2, el baricentro se llama punto medio del segmento que une $\bf A_{1}$ y $\bf A_{2}$. Para r = 3 se llama baricentro del triángulo, etc.

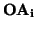
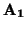
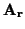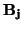
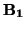
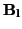
PROPOSICIÓN 2.4.4   Sean $\bf A_{1}$,...,$\bf A_{r}$ r puntos en un espacio afín $\mathbb {A}$ y sean a₁,..., a_r pesos. Supongamos que I₁,..., I_l son subconjuntos disjuntos de {1,..., r} cuya unión es {1,..., r}. Sea $\bf B_{j}$ el baricentro de los puntos {A_k : k $\in$ I_j} con los pesos correspondientes. 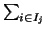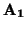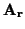Entonces el baricentro de {$\bf B_{1}$,...,$\bf B_{l}$} con pesos b_j = $\sum_{{i\in I_{j}}}^{}$a_i es exactamente el baricentro de {$\bf A_{1}$,...,$\bf A_{r}$} con pesos a₁,..., a_r.

Demostración. La dejamos como ejercicio interesante. (Es el típico problema de espacio afín de sustituir, sumar, combinar, resolver). $\qedsymbol$

De aquí se deduce que el baricentro de un triángulo es el baricentro del centro de masas de uno de los lados y el otro vértice. También que el baricentro de un cuadrilátero es el baricentro de los puntos medios de dos lados opuestos, etc.