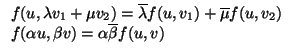Next: Definición de forma cuadrática
Up: Introducción
Previous: Introducción
Fijamos primero la notación: V es un espacio vectorial de dimensión finita y K es el cuerpo base, que
siempre supondremos es
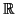 o
o
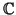 .
.
Definición 1.1.1
Una forma bilineal es una aplicación
f :
V×
V 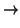 K
K
que es lineal en las dos componentes. Es decir, que si fijamos
v  V
V, se cumplen
pero: muy importante, no tienen por qué ser iguales!!!. En concreto, se dice que
Definición 1.1.2
La forma bilineal
f es
simétrica si para cualesquiera
u,
v  V
V, es
f (
u,
v) =
f (
v,
u).
La forma bilineal f es hemisimétrica o alternada si
f (u, v) = - f (v, u).
Por otro lado, puede ocurrir que
f (v, . ) = 0 (por ejemplo, para el vector 0 ocurre esto). En concreto: si
f cumple las dos condiciones siguientes:
entonces se dice que f es no degenerada.
Seguimos con las definiciones:
Definición 1.1.3
La forma bilineal
f es
definida si
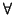 v
v  V
V no cero se tiene que
f (
v,
v)
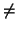
0.
PROPOSICIÓN 1.1.4
Si una forma bilineal f es definida, entonces es no degenerada.
Demostración.
Supongamos que es degenerada. Entonces hay un
u  V
V tal que
f (
u,
v) = 0 para todo
v o (por el otro lado),
hay un
v  V
V tal que
f (
u,
v) = 0 para todo
u. En el primer caso -y en el segundo lo mismo-, se
tendría que
f (
u,
u) = 0 y
f no podría ser definida.
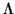
Nota: En espacios vectoriales reales, ninguna forma hemisimétrica es definida, pues
f (u, u) = - f (u, u)
y como puedo dividir por 2, tiene que ser f (u, u) = 0 para cualquier u.
Definición 1.1.5
Una forma bilineal definida es
definida positiva si
f (
u,
u) > 0 para todo
u  V
V. De la mima manera,
una forma bilineal definida es
definida negativa si
f (
u,
u) < 0 para todo
u  V
V.
Ejemplo 1.1.6
La forma
f (
u,
v) =
u1v1 +
u2v2 +
u3v3 es definida positiva en
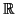 3
3, (es la que mide
distancias euclídeas), pero no lo es en
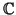 3
3: ejemplo,
F((1,
i, 0),(1,
i, 0)) = 0. Es decir, no
es definida si trabajamos en el cuerpo complejo. Pero en ambos casos, es no degenerada.
Ejemplo 1.1.7
Vamos a repasar unos cuantos ejemplos de formas bilineales. Tenemos el principal, que es el ``producto
escalar'' de dos vectores. En
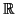 3
3, es una forma no degenerada definida positiva. Si consideramos
la misma forma sobre
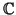 3
3, no es definida, pero no es degenerada.
Otro ejemplo: en
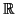 2, la forma
f ((u1, u2),(v1, v2)) = u1v1 - u2v2 es
hemisimétrica (por tanto no es definida) y es no degenerada.
2, la forma
f ((u1, u2),(v1, v2)) = u1v1 - u2v2 es
hemisimétrica (por tanto no es definida) y es no degenerada.
Otro: Sea V el espacio vectorial de las funciones continuas en [0, 1]. Se da:
es una forma bilineal simétrica definida positiva
(es muy importante que sean continuas, pues si no, no
es definida).
Ejemplo 1.1.8
MUY IMPORTANTE: Tomemos la aplicación
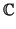 3× 3×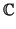 3 3 |
 |
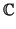 |
| ((u1, u2, u3),(v1, v2, v3) |
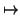 |
u1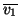 + u2 + u2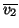 + u3 + u3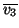 . . |
Esto no es una forma bilineal (en la segunda componente manda la conjugación). Pero es lo que se conoce como
forma
hermítica. Son las que se utilizan en la mecánica cuántica (son, de hecho, los
observables). Su definición -que hay que conocer- es:
Definición 1.1.9
Una aplicación
sesquilineal es la lineal en la primera y tal que
f (
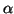 u
u,
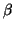 v
v) =
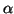
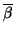 f
f (
u,
v). Evidentemente, esta definición sólo tiene sentido sobre los números complejos.
Una aplicación del producto V×V de un
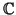 -espacio vectorial en
-espacio vectorial en
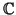 es una forma
hermítica si es una forma lineal en la primera componente y además,
f (u, v) =
es una forma
hermítica si es una forma lineal en la primera componente y además,
f (u, v) = 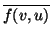 . De la definición se deduce que
. De la definición se deduce que
Son muy importantes y se comportan aproximadamente como las bilineales simétricas. Las veremos casi al
compás.



Next: Definición de forma cuadrática
Up: Introducción
Previous: Introducción
Pedro Fortuny Ayuso
2001-06-15
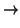 K
K
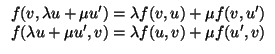
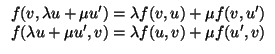
![$\displaystyle \begin{array}{l}
f(u,v)=0 \,\forall v\in V \Rightarrow v=0\\ [1ex] f(u,v)=0 \,\forall u\in V \Rightarrow u=0
\end{array}$](img15.gif)
![]() 2, la forma
f ((u1, u2),(v1, v2)) = u1v1 - u2v2 es
hemisimétrica (por tanto no es definida) y es no degenerada.
2, la forma
f ((u1, u2),(v1, v2)) = u1v1 - u2v2 es
hemisimétrica (por tanto no es definida) y es no degenerada.
![]() -espacio vectorial en
-espacio vectorial en
![]() es una forma
hermítica si es una forma lineal en la primera componente y además,
f (u, v) =
es una forma
hermítica si es una forma lineal en la primera componente y además,
f (u, v) = ![]() . De la definición se deduce que
. De la definición se deduce que