Next: Conceptos básicos
Up: FORMAS BILINEALES
Previous: FORMAS BILINEALES
Vamos a estudiar en este cuatrimestre dos asuntos importantes y peliagudos. Uno es el de las formas
bilineales. Es muy importante porque en física hay siempre un tipo de estructura bilineal trabajando. En
Teoría de la Relatividad, es la famosa métrica de Lorentz, mientras que en mecánica cuántica son
los ``observables''. La Teoría de la Relatividad se refiere a ``posiciones'' de cuerpos y movimientos
(cambios de lugar). Todo lo que hace referencia a una medida de posición se modeliza, matemáticamente, con
una métrica: el producto escalar usual no es más que la manera estandard de medir distancias (la
manera newtoniana). Einstein tiene la idea de introducir el ``tiempo'' en las coordenadas habituales. Ahí
entra la métrica de Lorentz.
En Cuántica se cambia el concepto de ``estado de una partícula'' por ``función de onda''. Y se
estudia todo lo que se refiere a los ``observables''. Un observable no es más -matemáticamente- que una
matriz hermítica (esto se sabe por confrontación con lo observado), y lo que se estudia son los
atuovalores y los autovectores, que vienen a ser los ``observables puros''. Una partícula tiene una
función de onda, que es una combinación compleja de los estados posibles (autovectores) y el colapso
de la función de onda no es más que una proyección en una base de vectores propios.
Comenzamos con un ejemplo que todos sabéis de C.O.U.: el producto vectorial. Fijamos un cuerpo: el real,
porque vamos a medir momentos, que son magnitudes reales. Fijamos también un espacio vectorial:
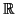 3, (el espacio normal y corriente). Sea M(u, v) la siguiente aplicación (las coordenadas
son en la base estandar):
3, (el espacio normal y corriente). Sea M(u, v) la siguiente aplicación (las coordenadas
son en la base estandar):
M : 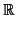 3× 3×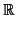 3 3 |
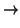 |
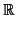 3 3 |
| (u, v) |
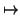 |
M(u, v) = det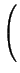 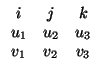  |
que, como todos sabéis, corresponde al momento angular (que es un vector perpendicular al plano en que gira
el eje) generado por una fuerza v en un eje u. Es evidente que, si sumo dos fuerzas o la multiplico por un
escalar, el momento sufre la misma transformación:
M(
u,
 v
v +
 w
w) =
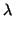 M
M(
u,
v) +
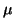 M
M(
u,
w),
y, que si considero una combinación de ejes (esto no sé muy bien físicamente cómo se representa),
ocurre lo mismo:
M(
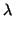 u
u +
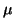 w
w,
v) =
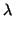 M
M(
u,
v) +
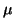 M
M(
w,
v)
(para verlo basta, por ejemplo, considerar las propiedades de los determinantes). Bien, esta M es una
aplicación de un producto de espacios vectoriales en un espacio vectorial, que se comporta de manera lineal
en las dos componentes. Esto es lo que se llama una aplicación bilineal. Si el espacio vectorial de
llegada es el cuerpo en el que se trabaja (v. gr.
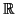 o
o
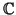 ), se llama forma
bilineal. El ejemplo típico es el producto escalar habitual: trabajamos en
), se llama forma
bilineal. El ejemplo típico es el producto escalar habitual: trabajamos en
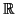 3 y definimos
3 y definimos
| |: 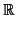 3× 3×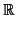 3 3 |
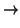 |
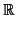 |
| (u, v) |
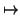 |
u1v1 + u2v2 + u3v3 |
que mide (físicamente no lo sé con precisión) una ``media ponderada de las longitudes y los
ángulos'' -más que nada diferencia cuándo dos vectores están en ángulo recto. Esta aplicación se
comporta exactamente igual que la del momento: es (pues llega a
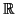 ) una forma bi-lineal.
) una forma bi-lineal.
Vistos dos ejemplos, pasamos a las definiciones precisas (pero quiero ver los ejemplos porque para los
físicos son lo único que existe).
Subsecciones



Next: Conceptos básicos
Up: FORMAS BILINEALES
Previous: FORMAS BILINEALES
Pedro Fortuny Ayuso
2001-06-15
![]() 3, (el espacio normal y corriente). Sea M(u, v) la siguiente aplicación (las coordenadas
son en la base estandar):
3, (el espacio normal y corriente). Sea M(u, v) la siguiente aplicación (las coordenadas
son en la base estandar):