Next: Matriz de una forma
Up: Introducción
Previous: Conceptos básicos
Es curioso que casi todas las formas bilineales que he escrito se puedan ``representar'' como (sumas de)
productos de grado dos de las coordenadas. En realidad no es tan curioso: al fin y al cabo, vamos a ver ahora
que es -casi- lo mismo dar un polinomio homogéneo de grado dos y una forma bilineal.
Definición 1.1.10
Una forma cuadrática sobre un espacio vectorial es una aplicación
| Q : V |
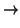 |
K |
| u |
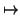 |
Q(u) |
tal que
Q(
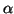 u
u) =
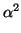 Q
Q(
v) y que además, la aplicación
| FQ : V×V |
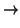 |
K |
| (u, v) |
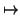 |
FQ(u, v) = 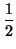 (Q(u + v) - Q(u) - Q(v)) (Q(u + v) - Q(u) - Q(v)) |
es una forma bilineal (que, evidentemente, es simétrica).
HASTA AQUÍ LA CLASE 1 (990210)
LEMA 1.1.11
Dada un forma bilineal
f :
V×
V 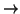 K
K, la apliación
| Qf : V |
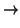 |
K |
| u |
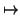 |
Qf(u) = f (u, u) |
es una forma cuadrática.
Demostración.
La demostración tiene dos partes: ver que
Qf(
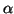 u
u) =
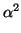 Qf
Qf(
u) (que es obvio) y ver que
FQf es una forma bilinieal (para lo que hay que ``echar una cuenta elemental'').
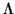
En particular, si f es simétrica y Q es la forma cuadrática asociada, siempre se tiene que
f = fQ. De modo que da lo mismo considerar formas bilineales simétricas y formas cuadráticas.
Para terminar el capítulo de definiciones preliminares, etc... noto que, si f es bilineal, la forma
fh(u, v) = (f (u, v) - f (v, u))
es bilineal hemisimétrica. Y que
f - fh
es bilineal simétrica. Es decir, toda forma bilineal es suma de una simétrica y una hemisimétrica. Esto
supongo que lo sabríais porque toda matriz cuadrada es suma de una simétrica y una hemisimétrica.
Está claro que si f es simétrica o hemisimétrica, los núcleos por la derecha y por la izquierda
coinciden y se llaman, sin más, ker(f ). También está claro que f es no degenerada si y sólo si
ambos núcleos son iguales al conjunto {0}.
Restricción de una forma bilineal a un subespacio. Dada una forma bilineal f sobre un espacio
vectorial V, si W es un subespacio de V, es evidente que se tiene una aplicación
f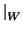 : W×W : W×W |
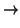 |
K |
| (u, v) |
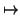 |
f (u, v) |
cuyo nombre es -de modo muy original- restricción de f a W. Si f es simétrica o
hemisimétrica y W = ker(f ), entonces,
f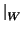 = 0. Si, por el contrario, W es complementario
de ker(f ), entonces
f
= 0. Si, por el contrario, W es complementario
de ker(f ), entonces
f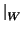 es no degenerada (evidentemente). Más ``difícil'' (o más
interesante) es demostrar que, dada una forma f bilineal cuyos núcleos por la izquierda y por la derecha
son iguales y dado un subespacio complementario de ambos, W, el conocimento de
f
es no degenerada (evidentemente). Más ``difícil'' (o más
interesante) es demostrar que, dada una forma f bilineal cuyos núcleos por la izquierda y por la derecha
son iguales y dado un subespacio complementario de ambos, W, el conocimento de
f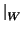 determina el de f. Esto se hace de manera directa:
determina el de f. Esto se hace de manera directa:
u =
u1 +
u2,
v =
v1 +
v2, con
ui 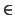
ker(
f ),
vi 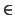 W
W
queremos calcular f (u, v) y es:



Next: Matriz de una forma
Up: Introducción
Previous: Conceptos básicos
Pedro Fortuny Ayuso
2001-06-15