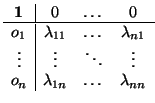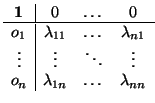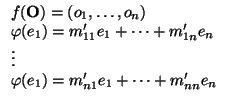LEMA 3.1.7
Sea
M una matriz
(
n + 1)×(
n + 1) de la forma de la definición anterior (es decir,
cuya primera fila es
(
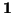
| 0 ... 0) y t. q. el adjunto del elemento (1, 1) es no
nulo). Existe
una única afinidad
(
f,
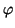
) de
(

,
V) cuya matriz asociada en
la referencia
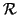
es precisamente
M.
Demostración.
Llamemos
M' = (
m'ij)
a la matriz
n×
n inferior derecha de
M. La aplicación (en
la referencia
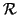
) dada por las ecuaciones
define de modo unívoco, por el corolario
1.5, una afinidad (que, por
construcción, tiene por matriz asociada a
M).
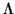
![]() ) una afinidad de
(
) una afinidad de
(![]() , V). En la referencia
, V). En la referencia
![]() , se escribirá:
, se escribirá: