


Next: Cambio de referencia y
Up: Transformaciones geométricas.
Previous: Matriz de una afinidad
Como se ha dicho, el conjunto de las afinidades de
 , que hemos llamado
G(
, que hemos llamado
G( ) forma un grupo cuya
operación es la composición de aplicaciones. Fijada una referencia, hemos asignado a cada elemento de
G(
) forma un grupo cuya
operación es la composición de aplicaciones. Fijada una referencia, hemos asignado a cada elemento de
G( ) una matriz de determinado tipo y viceversa: cada matriz de dicho tipo induce de manera
unívoca una afinidad. Es decir, hemos demostrado el siguiente
) una matriz de determinado tipo y viceversa: cada matriz de dicho tipo induce de manera
unívoca una afinidad. Es decir, hemos demostrado el siguiente
TEOREMA 3.1.8
Fijada una referencia

, existe una biyección entre el grupo de las afinidades de

y el conjunto de las matrices
(
n + 1)×(
n + 1) cuya primera fila es el vector
(1, 0,..., 0) y para las
que la matriz ``inferior derecha'' de tamaño
n×
n es inversible.
En realidad, el resultado es más fuerte y pasa por la siguiente proposición cuya demostración obviamos:
PROPOSICIÓN 3.1.9
El conjunto de las matrices
(n + 1)×(n + 1) cuya primera fila es
(1, 0,..., 0) y tales que la matriz
n×n ``inferior derecha'' es inversible, forma un grupo cuya operación es la multiplicación de
matrices. Este grupo se denomina ``grupo afín de dimensión n sobre K'' (donde K es el cuerpo
base) y se denota GAn(K).
Demostración.
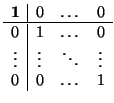
Aunque no demostremos el resultado entero, conviene conocer el elemento neutro y los inversos. Es elemental
comprobar que el elemento neutro es la matriz identidad:
Más complicado -aunque no lo vamos a hacer- es comprobar que toda matriz de
GAn(
K) tiene inverso en
GAn(
K). Dada
M  GAn
GAn(
K), si escribimos
entonces
M' es inversible y el inverso de
M es
donde

Y el teorema, en su versión definitiva, se enuncia
TEOREMA 3.1.10
Fijada una referencia

, existe un isomorfismo de grupos entre
G(

) y
GAn(
K).
Antes de estudiar el comportamiento de este isomorfismo por cambios de referen-cia, vamos a definir dos tipos
de afinidades ``especiales'', que dan -en cierto modo- una explicación a la aparición de las ``líneas
negras'' en las matrices.
Definición 3.1.11
La
traslación en
 de vector v
de vector v  V
V es la afinidad de

dada por la
siguiente aplicación:
Es trivial comprobar que una afinidad
(f, ) es una traslación si y sólo si su matriz asociada en
la referencia
) es una traslación si y sólo si su matriz asociada en
la referencia
 es de la forma
donde
(v1,..., vn) son las coordenadas de v en la base de la referencia
es de la forma
donde
(v1,..., vn) son las coordenadas de v en la base de la referencia
 . Está
claro que el inverso de la traslación de vector v es la traslación de vector - v.
. Está
claro que el inverso de la traslación de vector v es la traslación de vector - v.
Definición 3.1.12
Dado un punto



, se dice que una afinidad
(
f,

)
deja fijo 
si
f (

) =

. Se denota
G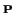
(

) al conjunto de afinidades de

que
dejan el punto

fijo.
Si  es el origen de la referencia
es el origen de la referencia
 , entonces una afinidad
(f,
, entonces una afinidad
(f, ) deja fijo
) deja fijo
 si y sólo si su matriz asociada en
si y sólo si su matriz asociada en
 es de la forma
donde, como siempre,
det(
es de la forma
donde, como siempre,
det(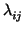 )
) 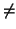 0.
0.
Sea  un punto cualquiera de
un punto cualquiera de
 . El siguiente teorema da una somera idea de la estructura del grupo de afinidades:
. El siguiente teorema da una somera idea de la estructura del grupo de afinidades:
TEOREMA 3.1.13
Cualquier afinidad es composición de una traslación y una afinidad que deja fijo el punto

.
Demostración.
Sea
(
f,

) una afinidad. Tomemos el vector
v =
f (

)

que une
f (

) con

y
sea
Tv la traslación de vector
v. Se tiene que
Tv(
f (

)) =
f (

) +
v =
f (

) +
f (

)

=

,
es decir, que la afinidad
Tvof deja fijo

. Por tanto, si
g =
Tvof, se tiene
(evidentemente) que
f = T-vog
donde
T-v es la traslación de vector -
v. Esto es precisamente lo que queríamos probar.




Next: Cambio de referencia y
Up: Transformaciones geométricas.
Previous: Matriz de una afinidad
Pedro Fortuny Ayuso
2001-06-15
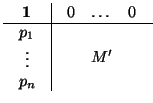
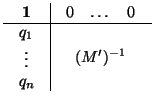
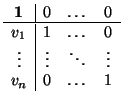
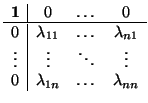
![]() un punto cualquiera de
un punto cualquiera de
![]() . El siguiente teorema da una somera idea de la estructura del grupo de afinidades:
. El siguiente teorema da una somera idea de la estructura del grupo de afinidades: