Cambio de referencia y matriz de una afinidad

Brevemente, puesto que la construcción es exactamente la misma que para espacios vectoriales, vamos a estudiar cómo varía la matriz de una afinidad cuando cambiamos la referencia afín. Partimos, por tanto, de un espacio afín ($\mathbb {A}$, V) y dos referencias $\mathcal {R}$ = ($\bf O$,(e₁,..., e_n)) y $\mathcal {R}$^$\prime$ = ($\bf O'$,(e'₁,..., e'_n)). Supongamos que la relación entre ambas referencias viene dada de la siguiente manera:

$$\left\{\vphantom{ \begin{array}{l} {\bf O'}=({o'}_{1},\dots,{o'}_... ...}\\ \vdots\\ e'_{n}=\mu _{n1}e_{1}+\dots+\mu _{nn}e_{n} \end{array}}\right.$$$$\begin{array}{l} {\bf O'}=({o'}_{1},\dots,{o'}_{n})\\ e'_{1}=\m... ...{1n}e_{n}\\ \vdots\\ e'_{n}=\mu _{n1}e_{1}+\dots+\mu _{nn}e_{n} \end{array}$$

es decir, que la matriz de paso de $\mathcal {R}$^$\prime$ a $\mathcal {R}$ es P:

P = $$\left(\vphantom{ \begin{array}{c\vert ccc} {\bf 1}& 0 & \dots & 0... ... \ddots & \vdots\\ o'_{n} & \mu _{1n} & \dots & \mu _{nn} \end{array}}\right.$$$$\begin{array}{c\vert ccc} {\bf 1}& 0 & \dots & 0\\ \hline o'_{1... ...\vdots & \ddots & \vdots\\ o'_{n} & \mu _{1n} & \dots & \mu _{nn} \end{array}$$$$\left.\vphantom{ \begin{array}{c\vert ccc} {\bf 1}& 0 & \dots & 0... ... \ddots & \vdots\\ o'_{n} & \mu _{1n} & \dots & \mu _{nn} \end{array}}\right)$$.

Sea (f,$\varphi$) una afinidad de $\mathbb {A}$. Supongamos que, en la referencia $\mathcal {R}$ su matriz es M:

M = $$\left(\vphantom{ \begin{array}{c\vert ccc} {\bf 1}& 0 & \dots & 0... ...ts & \ddots & \vdots\\ p_{n} & m _{1n} & \dots & m _{nn} \end{array}}\right.$$$$\begin{array}{c\vert ccc} {\bf 1}& 0 & \dots & 0\\ \hline p_{1}... ...s & \vdots & \ddots & \vdots\\ p_{n} & m _{1n} & \dots & m _{nn} \end{array}$$$$\left.\vphantom{ \begin{array}{c\vert ccc} {\bf 1}& 0 & \dots & 0... ...ts & \ddots & \vdots\\ p_{n} & m _{1n} & \dots & m _{nn} \end{array}}\right)$$.

Esto quiere decir que si $\bf Q$ es un punto de coordenadas (q₁,..., q_n) y (x₁,..., x_n) son las coordenadas de f ($\bf Q$) (ambos en la referencia $\mathcal {R}$), entonces

$$\left(\vphantom{ \begin{array}{c} {\bf 1}\\ \hline x_{1}\\ \vdots\\ x_{n} \end{array}}\right.$$$$\begin{array}{c} {\bf 1}\\ \hline x_{1}\\ \vdots\\ x_{n} \end{array}$$$$\left.\vphantom{ \begin{array}{c} {\bf 1}\\ \hline x_{1}\\ \vdots\\ x_{n} \end{array}}\right)$$ = $$\left(\vphantom{ \begin{array}{c\vert ccc} {\bf 1}& 0 & \dots & 0... ...ts & \ddots & \vdots\\ p_{n} & m _{1n} & \dots & m _{nn} \end{array}}\right.$$$$\begin{array}{c\vert ccc} {\bf 1}& 0 & \dots & 0\\ \hline p_{1}... ...s & \vdots & \ddots & \vdots\\ p_{n} & m _{1n} & \dots & m _{nn} \end{array}$$$$\left.\vphantom{ \begin{array}{c\vert ccc} {\bf 1}& 0 & \dots & 0... ...ts & \ddots & \vdots\\ p_{n} & m _{1n} & \dots & m _{nn} \end{array}}\right)$$$$\left(\vphantom{ \begin{array}{c} {\bf 1}\\ \hline q_{1}\\ \vdots\\ q_{n} \end{array}}\right.$$$$\begin{array}{c} {\bf 1}\\ \hline q_{1}\\ \vdots\\ q_{n} \end{array}$$$$\left.\vphantom{ \begin{array}{c} {\bf 1}\\ \hline q_{1}\\ \vdots\\ q_{n} \end{array}}\right)$$.

Para cambiar de referencia, hemos de sustituir (x₁,..., x_n) y (q₁,..., q_n) por las coordenadas de f ($\bf Q$) y $\bf Q$ en la referencia $\mathcal {R}$^$\prime$. Por las fórmulas del cambio de referencia afín, si las coordenadas de $\bf Q$ y f ($\bf Q$) en $\mathcal {R}$^$\prime$ son, respectivamente, (q'₁,..., q'_n) y (x'₁,..., x'_n), se tiene que

$$\left(\vphantom{ \begin{array}{c} {\bf 1}\\ \hline x_{1}\\ \vdots\\ x_{n} \end{array} }\right. \begin{array}{c} {\bf 1}\\ \hline x_{1}\\ \vdots\\ x_{n} \end{array} \left.\vphantom{ \begin{array}{c} {\bf 1}\\ \hline x_{1}\\ \vdots\\ x_{n} \end{array} }\right) \left(\vphantom{ \begin{array}{c\vert ccc} {\bf 1}& 0 & \dots & 0... ...& \ddots & \vdots\\ o'_{n} & \mu _{1n} & \dots & \mu _{nn} \end{array} }\right. \begin{array}{c\vert ccc} {\bf 1}& 0 & \dots & 0\\ \hline o'_{1} ... ...& \vdots & \ddots & \vdots\\ o'_{n} & \mu _{1n} & \dots & \mu _{nn} \end{array} \left.\vphantom{ \begin{array}{c\vert ccc} {\bf 1}& 0 & \dots & 0... ...& \ddots & \vdots\\ o'_{n} & \mu _{1n} & \dots & \mu _{nn} \end{array} }\right) \left(\vphantom{ \begin{array}{c} {\bf 1}\\ \hline x'_{1}\\ \vdots\\ x'_{n} \end{array} }\right. \begin{array}{c} {\bf 1}\\ \hline x'_{1}\\ \vdots\\ x'_{n} \end{array} \left.\vphantom{ \begin{array}{c} {\bf 1}\\ \hline x'_{1}\\ \vdots\\ x'_{n} \end{array} }\right)$$

$$\left(\vphantom{ \begin{array}{c} {\bf 1}\\ \hline q_{1}\\ \vdots\\ q_{n} \end{array} }\right. \begin{array}{c} {\bf 1}\\ \hline q_{1}\\ \vdots\\ q_{n} \end{array} \left.\vphantom{ \begin{array}{c} {\bf 1}\\ \hline q_{1}\\ \vdots\\ q_{n} \end{array} }\right) \left(\vphantom{ \begin{array}{c\vert ccc} {\bf 1}& 0 & \dots & 0... ...& \ddots & \vdots\\ o'_{n} & \mu _{1n} & \dots & \mu _{nn} \end{array} }\right. \begin{array}{c\vert ccc} {\bf 1}& 0 & \dots & 0\\ \hline o'_{1} ... ...& \vdots & \ddots & \vdots\\ o'_{n} & \mu _{1n} & \dots & \mu _{nn} \end{array} \left.\vphantom{ \begin{array}{c\vert ccc} {\bf 1}& 0 & \dots & 0... ...& \ddots & \vdots\\ o'_{n} & \mu _{1n} & \dots & \mu _{nn} \end{array} }\right) \left(\vphantom{ \begin{array}{c} {\bf 1}\\ \hline q'_{1}\\ \vdots\\ q'_{n} \end{array} }\right. \begin{array}{c} {\bf 1}\\ \hline q'_{1}\\ \vdots\\ q'_{n} \end{array} \left.\vphantom{ \begin{array}{c} {\bf 1}\\ \hline q'_{1}\\ \vdots\\ q'_{n} \end{array} }\right)$$

de donde

$$\left(\vphantom{ \begin{array}{c\vert ccc} {\bf 1}& 0 & \dots & 0... ...& \ddots & \vdots\\ o'_{n} & \mu _{1n} & \dots & \mu _{nn} \end{array} }\right. \begin{array}{c\vert ccc} {\bf 1}& 0 & \dots & 0\\ \hline o'_{1} ... ...& \vdots & \ddots & \vdots\\ o'_{n} & \mu _{1n} & \dots & \mu _{nn} \end{array} \left.\vphantom{ \begin{array}{c\vert ccc} {\bf 1}& 0 & \dots & 0... ...& \ddots & \vdots\\ o'_{n} & \mu _{1n} & \dots & \mu _{nn} \end{array} }\right) \left(\vphantom{ \begin{array}{c} {\bf 1}\\ \hline x'_{1}\\ \vdots\\ x'_{n} \end{array} }\right. \begin{array}{c} {\bf 1}\\ \hline x'_{1}\\ \vdots\\ x'_{n} \end{array} \left.\vphantom{ \begin{array}{c} {\bf 1}\\ \hline x'_{1}\\ \vdots\\ x'_{n} \end{array} }\right)$$ =

$$\left(\vphantom{ \begin{array}{c\vert ccc} {\bf 1}& 0 & \dots & 0... ...dots & \ddots & \vdots\\ p_{n} & m _{1n} & \dots & m _{nn} \end{array} }\right. \begin{array}{c\vert ccc} {\bf 1}& 0 & \dots & 0\\ \hline p_{1} &... ...dots & \vdots & \ddots & \vdots\\ p_{n} & m _{1n} & \dots & m _{nn} \end{array} \left.\vphantom{ \begin{array}{c\vert ccc} {\bf 1}& 0 & \dots & 0... ...dots & \ddots & \vdots\\ p_{n} & m _{1n} & \dots & m _{nn} \end{array} }\right) \left(\vphantom{ \begin{array}{c\vert ccc} {\bf 1}& 0 & \dots & 0... ...& \ddots & \vdots\\ o'_{n} & \mu _{1n} & \dots & \mu _{nn} \end{array} }\right. \begin{array}{c\vert ccc} {\bf 1}& 0 & \dots & 0\\ \hline o'_{1} ... ...& \vdots & \ddots & \vdots\\ o'_{n} & \mu _{1n} & \dots & \mu _{nn} \end{array} \left.\vphantom{ \begin{array}{c\vert ccc} {\bf 1}& 0 & \dots & 0... ...& \ddots & \vdots\\ o'_{n} & \mu _{1n} & \dots & \mu _{nn} \end{array} }\right) \left(\vphantom{ \begin{array}{c} {\bf 1}\\ \hline q'_{1}\\ \vdots\\ q'_{n} \end{array} }\right. \begin{array}{c} {\bf 1}\\ \hline q'_{1}\\ \vdots\\ q'_{n} \end{array} \left.\vphantom{ \begin{array}{c} {\bf 1}\\ \hline q'_{1}\\ \vdots\\ q'_{n} \end{array} }\right)$$

Despejando (1, x'₁,..., x'_n), al ser P la matriz de cambio de referencia, obtenemos, como siempre, que la matriz M' de (f,$\varphi$) en la referencia $\mathcal {R}$^$\prime$ es, precisamente

M' = P^-1MP.

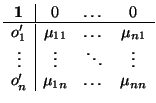
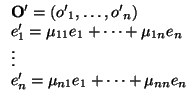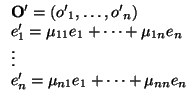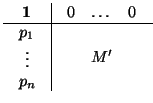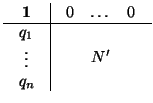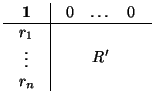Nota 3.1.14   Es importante darse cuenta de que el producto de dos matrices de GL_n(K), que ponemos

M = $$\left(\vphantom{ \begin{array}{c\vert c} {\bf 1}& \begin{array}{c... ...begin{array}{c} p_{1}\\ \vdots\\ p_{n} \end{array}& M' \end{array}}\right.$$$$\begin{array}{c\vert c} {\bf 1}& \begin{array}{ccc} 0 & \dots & 0... ...\hline \begin{array}{c} p_{1}\\ \vdots\\ p_{n} \end{array}& M' \end{array}$$$$\left.\vphantom{ \begin{array}{c\vert c} {\bf 1}& \begin{array}{c... ...begin{array}{c} p_{1}\\ \vdots\\ p_{n} \end{array}& M' \end{array}}\right)$$   y   N = $$\left(\vphantom{ \begin{array}{c\vert c} {\bf 1} & \begin{array}{... ...gin{array}{c} q_{1} \\ \vdots \\ q_{n} \end{array}& N' \end{array}}\right.$$$$\begin{array}{c\vert c} {\bf 1} & \begin{array}{ccc} 0 & \dots & ... ...line \begin{array}{c} q_{1} \\ \vdots \\ q_{n} \end{array}& N' \end{array}$$$$\left.\vphantom{ \begin{array}{c\vert c} {\bf 1} & \begin{array}{... ...gin{array}{c} q_{1} \\ \vdots \\ q_{n} \end{array}& N' \end{array}}\right)$$

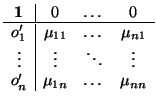
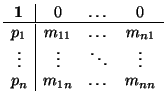
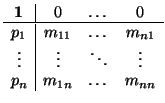
es una matriz del mismo tipo

MN = R = $$\left(\vphantom{ \begin{array}{c\vert c} {\bf 1} & \begin{array}{... ...gin{array}{c} r_{1} \\ \vdots \\ r_{n} \end{array}& R' \end{array}}\right.$$$$\begin{array}{c\vert c} {\bf 1} & \begin{array}{ccc} 0 & \dots & ... ...line \begin{array}{c} r_{1} \\ \vdots \\ r_{n} \end{array}& R' \end{array}$$$$\left.\vphantom{ \begin{array}{c\vert c} {\bf 1} & \begin{array}{... ...gin{array}{c} r_{1} \\ \vdots \\ r_{n} \end{array}& R' \end{array}}\right)$$

donde, y esto es lo importante, R' = M'N'. Digo esto porque cuando estudiemos las afinidades, vamos a ``simplificar'' siempre la matriz ``inferior derecha'' y podremos hacerlo precisamente porque la operación producto funciona en la matriz inferior derecha exactamente como el producto de matrices de tamaño n×n.