PROPOSICIÓN 3.1.15
Si
(
f,

) es una afinidad, entonces la imagen del baricentro de
k puntos es el baricentro de las
k
imágenes con los mismos pesos. Es más, si
f :

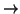

es una biyección que
conserva los baricentros, entonces es automáticamente una afinidad (i. e. existe un isomorfismo

de
V tal que
(
f,

) es una afinidad).
Demostración.
Sólo vamos a demostrar la primera parte. Supongamos que
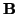
es el baricentro de
{
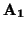
,...,
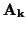
} con pesos
{
a1,...,
ak}. Entonces (por definición):
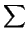
(
ai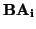
) = 0.
Por tanto,
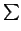 ai
ai
(
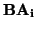
) = 0, pero, por ser
(
f,

) una afinidad,

(
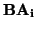
) =
f (
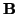
)
f (
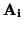
) y por tanto,
que significa precisamente que
f (
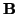
) es el baricentro de
{
f (
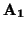
),...,
f (
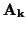
)} con
pesos
(
a1,...,
ak).

Demostración.
Si no hay puntos fijos,
S es vacío y es, por tanto, un subespacio afín. Supongamos que no es
vacío. Hay que comprobar que existen un punto



y un subespacio vectorial
E 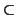 V
V tales que
S =
S(

,
E). Tomemos un punto

cualquiera de
S (que existe porque
S
no es vacío). Basta ver que la familia de vectores
E = {
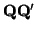
:
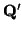
 S
S} es un subespacio
vectorial de
V. Sean, pues, dos vectores
v =
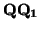
,
w =
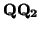
de dicha familia y sean

,

 K
K. Como

,
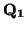
y
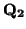
son puntos fijos, necesariamente

(
v) =
v y

(
w) =
w. Por tanto,

(
 v
v +
 w
w) =


(
v) +


(
w) =
 v
v +
 w
w. Esto implica que
f (

+
 v
v +
 w
w) =
f (

) +
 v
v +
 w
w =

+
 v
v +
 w
w. Por tanto, el punto

+
 v
v +
 w
w es fijo, para cualesquiera

,

 K
K y por ello
 v
v +
 w
w  E
E.
Así pues,
E es un subespacio
vectorial de
V, como queríamos comprobar.
