


Next: Ecuación de una simetría
Up: Transformaciones geométricas.
Previous: Continuamos con las afinidades
.
Vamos a hacer un estudio más o menos detallado de las afinidades
(f, ) tales que f2 = Id (que se
llaman involutivas).
) tales que f2 = Id (que se
llaman involutivas).
LEMA 3.1.17
Sea
(
f,

) una afinidad de

tal que
f2 =
Id. Para todo



, el
punto
3.1
es fijo (es decir, está en
Ef). Por tanto,
Ef no es vacío, en este caso.
Demostración.
Es una mera comprobación. Como
f es una afinidad, conserva baricentros, así que
f (
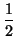

+
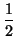 f
f (

)) =
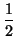 f
f (

) +
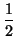 f
f (
f (

))
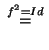
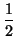 f
f (

) +
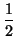

que es lo que queríamos ver. Como esto ocurre para todo



, necesariamente
Ef
es no vacío (salvo que

lo sea, cosa que suponemos falsa).

Por tanto, la imagen del punto  está totalmente determinada por el punto
está totalmente determinada por el punto
 = 1/2
= 1/2 + 1/2f (
+ 1/2f ( ). (El punto medio del segmento que une
). (El punto medio del segmento que une  con su imagen
f (
con su imagen
f ( ). Esto nos lleva,
de manera lógica a considerar el siguiente tipo de aplicaciones:
). Esto nos lleva,
de manera lógica a considerar el siguiente tipo de aplicaciones:
Definición 3.1.18 (Definición-proposición)
Sean
S =
S(

,
E) un subespacio afín propio (es decir, que no es el total ni el vacío) de

y
F  V
V un subespacio vectorial de
V complementario de
E (es decir,
V =
E 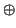 F
F). Dado



, el conjunto
S(

,
F)
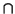 S
S(

,
E) está formado por un único punto (llamémosle

(

)). Se define la
proyección sobre S en la dirección de F como la apliación
Que se cortan en un sólo punto es consecuencia de la fórmula de las dimensiones y de que no son paralelos
(por construcción).
LEMA 3.1.19
Si

es la proyección sobre
S con dirección
F, como en la definición, entonces
- Dados
 ,
,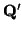

 , si
, si
 (
( ) =
) =  (
(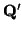 ), entonces
), entonces
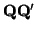
 F. Y
viceversa, si
F. Y
viceversa, si
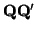
 F, entonces
F, entonces
 (
( ) =
) =  (
(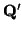 ).
).
 transforma subespacios afines de
transforma subespacios afines de
 en subespacios afines de S. Además, dado
en subespacios afines de S. Además, dado


 y un subespacio vectorial
E'
y un subespacio vectorial
E' 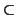 V, entonces
E'
V, entonces
E'  F = {0} si y sólo si
dim(
F = {0} si y sólo si
dim( (S(
(S( , E'))) = dim(S(
, E'))) = dim(S( , E')).
, E')).
Demostración.
Sean

,
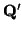


dos puntos con la misma imagen. Ahora bien,


(

)
 F
F y
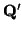

(
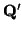
)
 F
F. Por tanto, como

(

) =

(
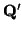
),
necesariamente el vector
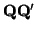
es
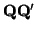
=


(

) +

(

)
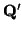
está en
F.
El recíproco es exactamente igual.
El segundo apartado lo dejamos sin demostrar.

LEMA 3.1.20
Si
(
f,

) es una afinidad cuyo cuadrado es la identidad (es decir,
f2 =
fof =
Id) y tomamos el subconjunto
de
V,
F =
L({
 f
f (

) :



}), entonces
F es un subespacio complementario de la
variedad de direcciones de
Ef. Si, además,

es la proyección sobre
Ef de dirección
F, entonces

(

) = 1/2

+ 1/2
f (

).
Demostración.
Es un subespacio vectorial por ser un linealizado. Veamos que es complementario de la variedad de direcciones
de
Ef. Primero hay que comprobar que la intersección de ambos es el vector 0. Sea
v  d
d (
Ef)
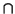 F
F. Puesto que
v  d
d (
Ef), se tiene que

(
v) =
v, al estar
Ef formado por puntos fijos. Por
otro lado
v =
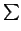
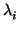
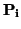 f
f (
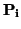
), al estar en
F. Como ya hemos visto que

(
v) =
v, debe ser (utilizando que
f2 =
Id):
v =
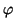
(
v) =
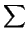
(
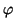
(
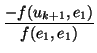
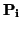 f
f (
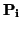
))) =
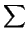
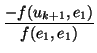 f
f (
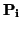
)
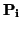
= -
v
de donde
v = -
v y, por tanto,
v = 0. Falta comprobar que todo vector de
V es suma de uno de
d (
Ef) con otro
de
F. Tomemos
v  V
V. Hay dos puntos

,

(en realidad hay infinitos) del espacio
afín

tales que
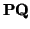
=
v. Por definición,

(

)

(

)
 d
d (
Ef) y como
sabemos que


(

) y


(

) están en
F, necesariamente se tiene que
 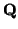 = =  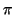 ( ( ) + ) + 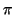 ( ( ) )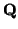 = =  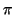 ( ( ) + ) + 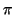 ( ( ) )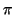 ( (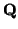 ) ) |
+ 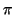 ( (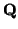 ) )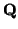 = = |
|
| |
= ( 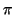 ( ( ) - ) - 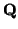 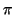 ( (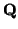 )) + )) + 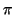 ( ( ) )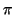 ( ( ) ) |
|
que es una suma de un vector de
F y otro de
Ef.
Para comprobar que
 (
( ) = 1/2
) = 1/2 + 1/2f (
+ 1/2f ( ), se razona como sigue: el punto
1/2
), se razona como sigue: el punto
1/2 + 1/2f (
+ 1/2f ( ) es fijo, por ser f involutiva. Por otro lado, dicho punto está en
S(
) es fijo, por ser f involutiva. Por otro lado, dicho punto está en
S( , F), pues
es el punto medio de
, F), pues
es el punto medio de  y
f (
y
f ( ). Como hemos visto que Ef y
S(
). Como hemos visto que Ef y
S( , F) sólo se cortan
en un punto, y a éste lo hemos llamado
, F) sólo se cortan
en un punto, y a éste lo hemos llamado
 (
( ), necesariamente ambos son iguales:
1/2
), necesariamente ambos son iguales:
1/2 + 1/2f (
+ 1/2f ( ) =
) =  (
( ).
).




Next: Ecuación de una simetría
Up: Transformaciones geométricas.
Previous: Continuamos con las afinidades
Pedro Fortuny Ayuso
2001-06-15
![]()
![]() (
(![]() ) = 1/2
) = 1/2![]() + 1/2f (
+ 1/2f (![]() ), se razona como sigue: el punto
1/2
), se razona como sigue: el punto
1/2![]() + 1/2f (
+ 1/2f (![]() ) es fijo, por ser f involutiva. Por otro lado, dicho punto está en
S(
) es fijo, por ser f involutiva. Por otro lado, dicho punto está en
S(![]() , F), pues
es el punto medio de
, F), pues
es el punto medio de ![]() y
f (
y
f (![]() ). Como hemos visto que Ef y
S(
). Como hemos visto que Ef y
S(![]() , F) sólo se cortan
en un punto, y a éste lo hemos llamado
, F) sólo se cortan
en un punto, y a éste lo hemos llamado
![]() (
(![]() ), necesariamente ambos son iguales:
1/2
), necesariamente ambos son iguales:
1/2![]() + 1/2f (
+ 1/2f (![]() ) =
) = ![]() (
(![]() ).
).
![]()