Next: Miscelánea ya dicha implícitamente
Up: Transformaciones geométricas.
Previous: Las afinidades cuyo cuadrado
Las afinidades cuyo cuadrado es la identidad tienen una matriz asociada (en una referencia bien escogida)
muy simple, como veremos a continuación. Fijemos lo necesario para definir una simetría: el eje y la
dirección de proyección. Sea, pues,
( , V) un espacio afín de dimensión n y E un
subespacio propio (ni el vacío ni el total) de
, V) un espacio afín de dimensión n y E un
subespacio propio (ni el vacío ni el total) de
 . Sea F un subespacio vectorial complementario de la variedad
de direcciones de E (a la que denotamos d (E)). Llamemos
. Sea F un subespacio vectorial complementario de la variedad
de direcciones de E (a la que denotamos d (E)). Llamemos 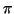 a la proyección de
a la proyección de
 sobre E de
dirección F y sea
f :
sobre E de
dirección F y sea
f : 
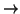
 la aplicación
g(
la aplicación
g( ) =
) =  + (2
+ (2
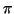 (
( )).
)).
Tomemos una referencia
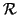 = (
= (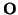 ,(e1,..., er, f1,..., fn-r)) donde
ei
,(e1,..., er, f1,..., fn-r)) donde
ei  d (E) y
fj
d (E) y
fj  F. Es elemental comprobar que un punto
F. Es elemental comprobar que un punto  de coordenadas
(p1,..., pn) se transforma, por g en
g(
de coordenadas
(p1,..., pn) se transforma, por g en
g( ) = (p1,..., pr,-pr+1,...,-pn) y, por tanto g
es una aplicación cuyas ecuaciones en la referencia
) = (p1,..., pr,-pr+1,...,-pn) y, por tanto g
es una aplicación cuyas ecuaciones en la referencia
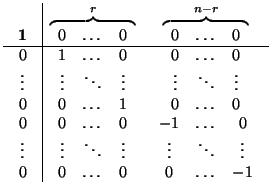
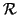 vienen determinadas por la matriz siguiente:
vienen determinadas por la matriz siguiente:
y, por tanto, g es una afinidad. Su cuadrado es la identidad porque
M(g,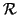 ) es la matriz
identidad. Es elemental comprobar que g es la simetría respecto de E en la dirección F.
) es la matriz
identidad. Es elemental comprobar que g es la simetría respecto de E en la dirección F.



Next: Miscelánea ya dicha implícitamente
Up: Transformaciones geométricas.
Previous: Las afinidades cuyo cuadrado
Pedro Fortuny Ayuso
2001-06-15
![]() = (
= (![]() ,(e1,..., er, f1,..., fn-r)) donde
ei
,(e1,..., er, f1,..., fn-r)) donde
ei ![]() d (E) y
fj
d (E) y
fj ![]() F. Es elemental comprobar que un punto
F. Es elemental comprobar que un punto ![]() de coordenadas
(p1,..., pn) se transforma, por g en
g(
de coordenadas
(p1,..., pn) se transforma, por g en
g(![]() ) = (p1,..., pr,-pr+1,...,-pn) y, por tanto g
es una aplicación cuyas ecuaciones en la referencia
) = (p1,..., pr,-pr+1,...,-pn) y, por tanto g
es una aplicación cuyas ecuaciones en la referencia
![]() vienen determinadas por la matriz siguiente:
vienen determinadas por la matriz siguiente: