Breves nociones sobre ángulos no orientados.

Fijemos dos vectores u, v de un espacio vectorial métrico V. Supongamos que ninguno de ellos es nulo. Por la desiguladad de Schwarz,

|< u, v >|$$\leq$$|u||v|,

de donde

-1 $$\leq$$ $${\frac{{<u,v>}}{{\vert u \vert \vert v \vert }}}$$ $$\leq$$ 1.

Se llama ángulo no orientado que forman u y v y se denota $\hat{{uv}}$ al único $\alpha$ $\in$ [0,$\pi$] tal que

cos($$\alpha$$) = $${\frac{{<u,v>}}{{\vert u \vert \vert v \vert }}}$$.

Las propiedades básicas son

• $\hat{{uv}}$ = $\hat{{vu}}$.
• Dos vectores u, v son linealmente independientes si y sólo si $\pi$ $\neq$ $\hat{{uv}}$ $\neq$ 0.
• Dos vectores son ortogonales si y sólo si $\hat{{uv}}$ = $\pi$/2.

Esto es una explicación muy somera, pero suficiente para lo que necesitamos.

TEOREMA 3.2.6 (Teorema del coseno)   Sean u, v $\in$ V. Entonces

(u + v)² = u² + v² + 2 < u, v > =|u$$\vert^{{2}}_{}$$ +|v$$\vert^{{2}}_{}$$ + 2|u||v|cos($$\hat{{uv}}$$).

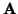
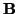
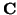
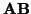
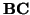
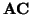
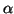
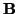
Nota 3.2.7   Atención a la fórmula anterior porque es relativa a vectores. Si nos situamos en un espacio euclídeo (es decir, un espacio de puntos) y $\bf A$,$\bf B$,$\bf C$ son tres puntos (que determinan un triángulo) y tomamos v = $\bf AB$, w = $\bf BC$, t = $\bf AC$ y $\alpha$ es ``el ángulo'' en $\bf B$, entonces es

$$\bf AC^{{2}}_{}$$ = $$\bf AB^{{2}}_{}$$ + $$\bf BC^{{2}}_{}$$ - 2|$$\bf AB$$||$$\bf BC$$|cos$$\alpha$$

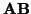
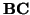
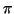
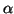
porque realmente los vectores $\bf AB$ y $\bf BC$ forman un ángulo $\pi$ - $\alpha$, ``pues hay que ponerlos con vértice común''.

TEOREMA 3.2.8 (Teorema de Pitágoras)   Dados dos vectores u, v ortogonales, se tiene que

|u + v$$\vert^{{2}}_{}$$ =|u$$\vert^{{2}}_{}$$ +|v$$\vert^{{2}}_{}$$.