


Next: Breves nociones sobre ángulos
Up: ESPACIOS AFINES Y MÉTRICOS
Previous: Ejemplos de afinidades: en
Hasta ahora hemos estudiado el espacio afín como mero conjunto de puntos con una estructura ``lineal''
heredada del espacio vectorial subyacente. Pero para obtener una buena imagen de la realidad hay que utilizar
algún concepto más. En concreto, es ya el momento de introducir las formas bilineales para estudiar la
geometría del espacio. Una forma bilineal simétrica no es más, recuerdo, que la generalización de
la noción de producto escalar.
Así pues, fijamos un espacio vectorial V sobre los números reales, de dimensión n. Sea también
 un espacio afín sobre V.
un espacio afín sobre V.
Definición 3.2.1
Un
espacio vectorial métrico es un par (
V,
g) donde
g es una forma bilineal simétrica definida
positiva. Un
espacio euclídeo (o
espacio afín euclídeo) es un espacio afín

cuyo espacio vectorial subyacente tiene asociada una forma bilineal definida positiva (es decir,
que es un e. v. métrico).
Habitualmente, como la forma bilineal g será fija, utilizaremos la siguiente notación: si u, v  V son
vectores, entonces < u, v > es, por definición, g(u, v) y
u2 = < u, u >. La matriz de g en una base se
escribirá, como es habitual, (gij). Por el teorema de Gram-Schmidt, sabemos que existe un base de V
que es ortonormal para g. Siempre que tomemos un espacio vectorial euclídeo, supondremos (salvo que se
diga lo contrario) que hemos fijado una base ortonormal. Llamaremos producto escalar a la forma bilineal
g.
V son
vectores, entonces < u, v > es, por definición, g(u, v) y
u2 = < u, u >. La matriz de g en una base se
escribirá, como es habitual, (gij). Por el teorema de Gram-Schmidt, sabemos que existe un base de V
que es ortonormal para g. Siempre que tomemos un espacio vectorial euclídeo, supondremos (salvo que se
diga lo contrario) que hemos fijado una base ortonormal. Llamaremos producto escalar a la forma bilineal
g.
Definición 3.2.2
El
módulo de un vector
v  V
V es
|
v|=
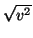
. Está claro que si escribimos
v
en una base ortonormal,
v = (
v1,...,
vn), entonces
|
v|=
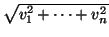
.
LEMA 3.2.3 (Propiedades inmediatas del módulo)
El módulo cumple las siguientes propiedades:
- Para todo v de V se tiene
|v|
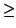 0 y, de hecho,
|v|= 0 si y sólo si v = 0.
0 y, de hecho,
|v|= 0 si y sólo si v = 0.
- Para todo v de V y todo escalar
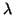 ,
|
,
|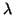 v|=|
v|=|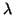 ||v|.
||v|.
- Si u, v son linealmente dependientes, entonces
|u||v|= < u, v >.
- Si u, v son linealmente independientes, entonces
|u||v|>|< u, v >|. Esta propiedad, junto con la anterior se escribe
|u||v|
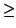 |< u, v >| y
se llama desigualdad de Schwartz.
|< u, v >| y
se llama desigualdad de Schwartz.
- Para u, v
 V, es
|u + v|
V, es
|u + v|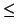 |u|+|v|. (Desigualdad triangular).
|u|+|v|. (Desigualdad triangular).
La demostración es muy sencilla y no la hago. Compensa que las intentéis hacer por vosotros mismos.
Definición 3.2.4
Sea
E = (

,
V) un espacio euclídeo. Dados dos puntos
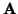
,
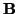
, se llama
distancia
de 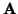 a
a 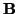
al módulo del vector
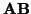
, es decir:
En un espacio euclídeo, se llama referencia ortonormal a una referencia
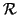 = (
= (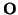 ,(e1,..., en)) tal que la base
(e1,..., en) de V es ortonormal para el producto
escalar. Fijada una referencia ortonormal, es claro que si dos puntos
,(e1,..., en)) tal que la base
(e1,..., en) de V es ortonormal para el producto
escalar. Fijada una referencia ortonormal, es claro que si dos puntos
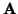 ,
,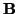 tienen respectivamente
coordenadas
(a1,..., an) y
(b1,..., bn), entonces
tienen respectivamente
coordenadas
(a1,..., an) y
(b1,..., bn), entonces
|
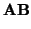
|=
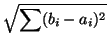
.
Subsecciones



Next: Breves nociones sobre ángulos
Up: ESPACIOS AFINES Y MÉTRICOS
Previous: Ejemplos de afinidades: en
Pedro Fortuny Ayuso
2001-06-15
![]() un espacio afín sobre V.
un espacio afín sobre V.