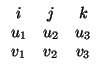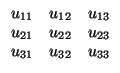Noción de orientación. Gram-Schmidt orientado. Producto vectorial.

A partir de ahora, vamos a necesitar de modo habitual la noción de orientación de una base respecto de otra. Partimos de un espacio vectorial V y una base fija $\mathcal {B}$ = (e₁,..., e_n). Dada otra base $\mathcal {B}$ = (e'₁,..., e'_n), diremos que $\mathcal {B}$ tiene la misma orientación que $\mathcal {B}$ si el determinante de la matriz de cambio de base P es positivo.

En la construcción de la base de Gram-Schmidt hay una ambigüedad cuando se normaliza (se puede tomar la raíz cuadrada positiva o negativa del módulo de los nuevos vectores). Si se impone una condición más, se tiene la unicidad:

TEOREMA 3.2.9 (Re-enunciado de Gram-Schmidt) Sea f una forma bilineal simétrica definida positiva en un espacio vectorial real de dimensión n y sea $\mathcal {B}$ = (e₁,..., e_n) una base de V. Existe una única base $\mathcal {B}$ = (e'₁,..., e'_n) de V tal que

< e'₁,..., e'_r > = < e₁,..., e_r > parar = 1...n.

y tal que los sistemas (e₁,..., e_r) y (e'₁,..., e'_r) tienen la misma orientación para r = 1...n.

La construcción de esta base se hace por el procedimiento que os expliqué de ``triangularizar'' la matriz mediante operaciones por columnas y, una vez hecho, normalizar la base ortogonal que se encuentra tomando las raíces positivas de los módulos de los vectores.

Para definir el producto vectorial necesitamos que el espacio vectorial sea de dimensión 3. Lo suponemos de ahora en adelante. Sea $\mathcal {B}$ = (e₁, e₂, e₃) una base.

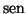
Definición 3.2.10 Dados dos vectores linealmente independientes u, v $\in$ V, definimos el producto vectorial de u con v (en este orden) como el vector u×v de V cuyo módulo es |u||v| $\sen$ ( $\hat{{uv}}$ ), que es ortogonal a u y v y tal que la base (u, v, u×v) tiene la misma orientación que $\mathcal {B}$ . Si u y v son linealmente dependientes, su producto vectorial es, por definición 0.

La expresión analítica del producto vectorial es la siguiente: llamemos e₁ = i, e₂ = j, e₃ = k; si u = (u₁, u₂, u₃) y v = (v₁, v₂, v₃), entonces

u×v = $\displaystyle \left\vert\vphantom{ \begin{array}{ccc} i & j & k\\ u_{1} & u_{2} & u_{3}\\ v_{1} & v_{2} & v_{3} \end{array}}\right.$ $\displaystyle \begin{array}{ccc} i & j & k \\ u_{1} & u_{2} & u_{3}\\ v_{1} & v_{2} & v_{3} \end{array}$ $\displaystyle \left.\vphantom{ \begin{array}{ccc} i & j & k\\ u_{1} & u_{2} & u_{3}\\ v_{1} & v_{2} & v_{3} \end{array}}\right\vert$ .

Definición 3.2.11 El producto mixto de tres vectores u₁, u₂, u₃, que se denotará [u₁, u₂, u₃], se define:

[u₁, u₂, u₃] = < u₁, u₂×u₃ > .

[u₁, u₂, u₃] = = $\displaystyle \left\vert\vphantom{ \begin{array}{ccc} u_{11} & u_{12} & u_{13}\\ u_{21} & u_{22} & u_{23}\\ u_{31} & u_{32} & u_{33} \end{array}}\right.$ $\displaystyle \begin{array}{ccc} u_{11} & u_{12} & u_{13}\\ u_{21} & u_{22} & u_{23}\\ u_{31} & u_{32} & u_{33} \end{array}$ $\displaystyle \left.\vphantom{ \begin{array}{ccc} u_{11} & u_{12} & u_{13}\\ u_{21} & u_{22} & u_{23}\\ u_{31} & u_{32} & u_{33} \end{array}}\right\vert$

Continuamos en el espacio vectorial real tridimensional V dotado de una forma bilineal simétrica g.

Definición 3.2.12 Dados dos subconjuntos S₁, S₂ 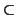$\subset$ V, la distancia de S₁ a S₂ es el extremo inferior de las distancias entre pares de puntos de S₁ y S₂. Esto es:

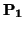
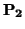
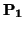
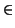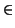d (S₁, S₂) = inf{d ( $\displaystyle \bf P_{1}$ , $\displaystyle \bf P_{2}$ ) : $\displaystyle \bf P_{1}$ $\displaystyle \in$ S₁, $\displaystyle \bf P_{2}$ $\displaystyle \in$ S₂}.

PROPOSICIÓN 3.2.13 Suongamos que los subconjuntos S₁ y S₂ son subespacios afines de V. Entonces

S₁ y S₂ se cortan si y sólo si su distancia es 0.
Existen $\bf A_{1}$ $\in$ S₁ y $\bf A_{2}$ $\in$ S₂ tales que d (S₁, S₂) = d ( $\bf A_{1}$ , $\bf A_{2}$ ) =| $\bf A_{1}A_{2}$ |.
Si S₁ = S( $\bf P_{1}$ , E₁) y S₂ = S( $\bf P_{2}$ , E₂), entonces d (S₁, S₂) =|( $\bf P_{1}P_{2}$ )_v| donde ( $\bf P_{1}P_{2}$ )_v es la componente vertical de $\bf P_{1}P_{2}$ relativa a E₁ + E₂.