Definición 3.3.1
Sean (
V,
g) y (
W,
g') dos espacios vectoriales métricos. Una
isometría entre ellos es un
isomorfismo
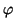
:
V 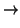 W
W
tal que para todos
v1,
v2  V
V se tiene que
g(
v1,
v2) =
g'(

(
v1),

(
v2)). En
particular, si < , > es un producto escalar en
V, llamamos isometría de
V a todo automorfismo

de
V tal que
<
v1,
v2 > = <

(
v1),

(
v2) >, para cualesquiera
v1,
v2.
Nota 3.3.3
Tomemos una base
(
e1,...,
en) de
V. Supongamos que la matriz de < , > en dicha base es (
gij)
(no estamos suponiendo que la base es ortonormal). Sea

un endomorfismo de
V cuya matriz en la
base anterior es
N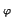
. El endomorfismo

es una
isometría si y sólo si cumple las dos
propiedades siguientes:
La segunda condición, puesto que
det((
gij))
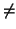
0 (al ser definida positiva), se puede resumir en que
det(
N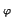
)
2 = 1, es decir,
det(
N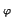
) = ±1, que
implica automáticamente que
N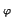
es inversible. Por tanto, un endomorfismo

es una isometría si y sólo si existe una base para
la que
N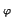 t
t(
gij)
N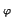
= (
gij), donde (
gij) y
N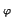
son las matrices de
la métrica y de la apliación en dicha base.
![]() V.
V.