< 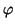 (
(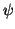 (u)),
(u)),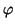 (
(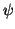 (v)) > = <
(v)) > = < 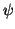 (u),
(u),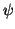 (v) > = < u, v >
(v) > = < u, v >
(la primera igualdad porque
a) La aplicación f deja un punto fijo, digamos
f (![]() ) =
) = ![]() . Para construir el automorfismo
asociado, definimos
. Para construir el automorfismo
asociado, definimos
![]() : V
: V ![]() V como
V como
![]() (v) = (f (
(v) = (f (![]() )f (
)f (![]() + v)) =
+ v)) = ![]() f (
f (![]() + v). Está claro que
+ v). Está claro que ![]() es una aplicación (está bien definida). Además,
es una aplicación (está bien definida). Además,
![]() (0) = 0, por construcción. Sean ahora u, v
(0) = 0, por construcción. Sean ahora u, v ![]() V. Se tiene que
V. Se tiene que
| d (f ( |
f ( |
|
| =|( |
b) Si f no deja ningún punto invariante, entonces existe una traslación Tv tal que
foTv deja fijo algún punto ![]() . Por el apartado a),
foTv es un movimiento. Por tanto, como
las traslaciones son movimientos (pues su automorfismo asociado es la identidad, que es una isometría)
y puesto que la composición de movimientos es un movimiento,
la aplicación
foTvoT-v es un movimiento, pero
foTvoT-v = f, así que
f es un movimiento.
. Por el apartado a),
foTv es un movimiento. Por tanto, como
las traslaciones son movimientos (pues su automorfismo asociado es la identidad, que es una isometría)
y puesto que la composición de movimientos es un movimiento,
la aplicación
foTvoT-v es un movimiento, pero
foTvoT-v = f, así que
f es un movimiento.