TEOREMA 3.4.2
En las mismas condiciones que antes, si
(
e1,...,
en) es una base ortonormal de
E y el
hiperparalelepípedo es de dimensión
n (es decir, viene dado por el punto
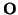
y la familia
{
u1,...,
un}) y se
escribe
ui =
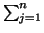 aijej
aijej, entonces
Vol (H) =|det(aij)|.
Nota 3.4.3
Un triángulo con vértice en
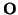
y cuyos lados en
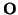
son los vectores
u1,
u2,
tiene por volumen (área) la mitad del paralelogramo
H = {
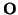
,{
u1,
u2}}. Un tetraedro tiene
por volumen 1/6 del paralelepípedo correspondiente.
Nota 3.4.4
Si
v1,
v2,
v3 son tres vectores en el espacio euclídeo
V de dimensión 3 y
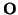
es un punto, entonces el área del paralelogramo
{
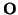
,{
v1,
v2}} es:
Vol ({
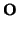
,{
v1,
v2}}) =|
v1×
v2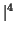
(donde × indica el producto vectorial). El volumen de
H = {
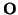
,{
v1,
v2,
v3}} viene dado por
Vol ({
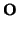
,{
v1,
v2,
v3}} =|[
v1,
v2,
v3]|.
donde los corchetes indican el producto mixto.
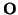 ,{u1,..., ur-1}) . |vr|. Donde vr
es la componente vertical de ur respecto del subespacio
L({u1,..., ur-1}).
,{u1,..., ur-1}) . |vr|. Donde vr
es la componente vertical de ur respecto del subespacio
L({u1,..., ur-1}).