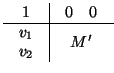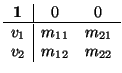Next: Anexo: áreas y volúmenes
Up: Isometrías y Movimientos.
Previous: Isometrías de tipo b)
Una vez estudiadas las isometrías del plano, la descripción de los movimientos es elemental:
TEOREMA 3.3.15
Cualquier movimiento del plano es del tipo siguiente:
- Un giro.
- Una simetría.
- Una traslación.
- La composición de un giro con una traslación.
- La composición de una traslación con un giro.
- La composición de una simetría con una traslación.
- La composición de una traslación con una simetría.
Demostración.
Esto es consecuencia de que todo movimento es composición de una traslación con un movimiento que deja
fijo un punto. Como ya vimos, los que dejan fijo un punto se pueden identificar con las isometrías,
así que (hablando con cierta imprecisión), todo movimiento es producto de una traslación y una
isometría. Si no hay traslación estamos en los dos primeros casos, y si la hay, en los cinco últimos.

Nota 3.3.16
Es muy importante el orden. No es lo mismo primero trasladar y luego girar que primero girar y luego
trasladar.
Pero, de hecho, el teorema anterior no dice todo. Vamos a estudiar todos los movimientos en función de la
orientación y de los puntos fijos. Tomemos, pues
f :  2
2 
 2 un
movimiento y llamemos
2 un
movimiento y llamemos  a su isometría asociada. Según la orientación, hay dos
posibilidades: que la conserve o que no. Supongamos primero que la conserva.
a su isometría asociada. Según la orientación, hay dos
posibilidades: que la conserve o que no. Supongamos primero que la conserva.
Movimientos que conservan la orientación.
Tenemos, pues, un movimiento
(f, ) directo. En una referencia ortonormal, su matriz será
) directo. En una referencia ortonormal, su matriz será
Hay un caso especial:
cos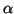 = 1: la isometría asociada es la
identidad, así que el movimento es una traslación (o la identidad, si
v1 = v2 = 0).
= 1: la isometría asociada es la
identidad, así que el movimento es una traslación (o la identidad, si
v1 = v2 = 0).
Si
cos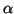
 1, se comprueba que f tiene un único punto fijo (ejercicio IMPORTANTE), digamos
1, se comprueba que f tiene un único punto fijo (ejercicio IMPORTANTE), digamos  . Si cambiamos de referencia y tomamos
. Si cambiamos de referencia y tomamos

 una ortonormal centrada en
una ortonormal centrada en  , entonces la
matriz de f en
, entonces la
matriz de f en

 es
es
(pues el origen de

 es fijo y la matriz de la isometría no cambia si las bases son
ortonormales). Por tanto, f es exactamente el giro de ángulo
es fijo y la matriz de la isometría no cambia si las bases son
ortonormales). Por tanto, f es exactamente el giro de ángulo 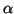 centrado en
centrado en  .
.
Movimientos que cambian la orientación
Supongamos ahora que f es un movimiento inverso (es decir, la isometría  es una
simetría). En una referencia
es una
simetría). En una referencia
 ortonormal, la matriz de f será
ortonormal, la matriz de f será
Puede ocurrir que f tenga o no puntos fijos.
1.- Supongamos primero que f tiene puntos fijos. Sea  uno de ellos. Por la sección anterior, sabemos
que existe una referencia
uno de ellos. Por la sección anterior, sabemos
que existe una referencia

 tal que la matriz de f en
tal que la matriz de f en

 es
es
(tomando como origen de

 el punto
el punto  ). Por tanto, no sólo tiene un punto fijo, sino
que hay toda una recta de puntos fijos. En concreto, si la base de
). Por tanto, no sólo tiene un punto fijo, sino
que hay toda una recta de puntos fijos. En concreto, si la base de

 es
(e'1, e'2), entonces
la recta de puntos fijos es
r =
es
(e'1, e'2), entonces
la recta de puntos fijos es
r =  +
+  e'1. Por tanto, el movimiento es la simetría ortogonal
respecto de la recta
e'1. Por tanto, el movimiento es la simetría ortogonal
respecto de la recta
 +
+  e'1.
e'1.
2.- La otra posibilidad es que f no tenga puntos fijos. Tomando una base
(e1, e2), podemos suponer que la
matriz de f es
La isometría  tiene (como se vio) dos rectas invariantes (en estas coordenadas, las rectas
< e1 > y < e2 >). Por tanto, el movimiento puede tener rectas invariantes en dichas direcciones. Veamos si hay
alguna en la segunda dirección (paralela a x = 0; es decir, de la forma x = k): hemos de ver si el
siguiente sistema3.3 tiene alguna solución en k
y -se comprueba- que la única posible es k = 0, cuando v1 = 0. En la otra dirección (la dada por < e1 >), el
sistema correspondiente en k es
y -se comprueba- que tiene la solución k = v2/2. Es decir, la recta
tiene (como se vio) dos rectas invariantes (en estas coordenadas, las rectas
< e1 > y < e2 >). Por tanto, el movimiento puede tener rectas invariantes en dichas direcciones. Veamos si hay
alguna en la segunda dirección (paralela a x = 0; es decir, de la forma x = k): hemos de ver si el
siguiente sistema3.3 tiene alguna solución en k
y -se comprueba- que la única posible es k = 0, cuando v1 = 0. En la otra dirección (la dada por < e1 >), el
sistema correspondiente en k es
y -se comprueba- que tiene la solución k = v2/2. Es decir, la recta
r : y = v2/2
es invariante. Obsérvese, además, que r es paralela al eje de simetría. Si tomamos el punto  en
esta recta y consideramos
en
esta recta y consideramos

 = {(e1, e2)}, la matriz de f en
= {(e1, e2)}, la matriz de f en

 es
y el movimiento es la composición de la simetría respecto de la recta
es
y el movimiento es la composición de la simetría respecto de la recta
 +
+  e1 con
la traslación de vector
v1/2e1, que es paralela al eje de simetría. Por tanto, si v1 = 0, tendríamos puntos fijos, cosa que estamos suponiendo falsa.
e1 con
la traslación de vector
v1/2e1, que es paralela al eje de simetría. Por tanto, si v1 = 0, tendríamos puntos fijos, cosa que estamos suponiendo falsa.
Conclusión: clasificación de los movimientos en
 2.
2.
De todo lo dicho se deduce la siguiente clasificación. Tomamos un movimiento f de
 2. Sea
M su matriz en una referencia ortonormal cualquiera
2. Sea
M su matriz en una referencia ortonormal cualquiera
 = (
= ( ,(e1, e2)):
,(e1, e2)):
Llamemos
d = det(M) y
t = m11 + m22 (la traza de  ). Sea v el vector
v = (v1, v2) (que es la
traslación asociada a f). Se tiene una posibilidad (y sólo una) de las siguientes:
). Sea v el vector
v = (v1, v2) (que es la
traslación asociada a f). Se tiene una posibilidad (y sólo una) de las siguientes:
Además, se tiene que
LEMA 3.3.17
La composición de dos simetrías respecto de ejes que se cortan es un giro. La composición de dos
simetrías de ejes paralelos es una traslación.
No lo demostramos: ejercicio fácil sabiendo el resultado ``paralelo'' de isometrías y teniendo un poco
de cuidado.
Por tanto, se tiene el siguiente
TEOREMA 3.3.18
Todo movimiento del plano euclídeo se puede escribir como composición de 3 simetrías.
Demostración.
No hay ya nada que probar, pues por la tabla anterior, o es un giro (en cuyo caso es composición de
dos simetrías, o es una simetría y (eventualmente) una traslación, en cuyo caso es
composición de tres simetrías.




Next: Anexo: áreas y volúmenes
Up: Isometrías y Movimientos.
Previous: Isometrías de tipo b)
Pedro Fortuny Ayuso
2001-06-15
![]() ) directo. En una referencia ortonormal, su matriz será
) directo. En una referencia ortonormal, su matriz será
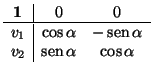
![]()
![]() 1, se comprueba que f tiene un único punto fijo (ejercicio IMPORTANTE), digamos
1, se comprueba que f tiene un único punto fijo (ejercicio IMPORTANTE), digamos ![]() . Si cambiamos de referencia y tomamos
. Si cambiamos de referencia y tomamos
![]()
![]() una ortonormal centrada en
una ortonormal centrada en ![]() , entonces la
matriz de f en
, entonces la
matriz de f en
![]()
![]() es
es
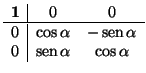
![]() es una
simetría). En una referencia
es una
simetría). En una referencia
![]() ortonormal, la matriz de f será
ortonormal, la matriz de f será

![]() uno de ellos. Por la sección anterior, sabemos
que existe una referencia
uno de ellos. Por la sección anterior, sabemos
que existe una referencia
![]()
![]() tal que la matriz de f en
tal que la matriz de f en
![]()
![]() es
es

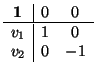
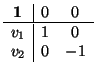
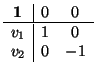
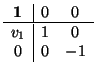
![]() 2.
2.
![]() 2. Sea
M su matriz en una referencia ortonormal cualquiera
2. Sea
M su matriz en una referencia ortonormal cualquiera
![]() = (
= (![]() ,(e1, e2)):
,(e1, e2)):