


Next: Formas canónicas de las
Up: Resultados generales
Previous: Resultados generales
Antes de estudiar las cónicas y las cuádricas, conviene demostrar un resultado muy útil, con el que
podremos expresar cualquier forma cuadrática definida en un espacio métrico en su forma diagonal, con una
base ortonormal. El resultado se aplica también (y esto es importantísimo para la mecánica
cuántica) a formas bilineales simétricas definidas en espacios vectoriales hermíticos (espacios
vectoriales dotados de una forma hermítica). Lo vamos a enunciar para los dos tipos de espacios, pero
sólo vamos a hacer la demostración en el caso euclídeo (es decir, sobre el cuerpo real). En concreto,
el resultado es el siguiente
TEOREMA 4.1.1
Sea
E un espacio vectorial de dimensión finita sobre el cuerpo

ó
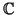
. Sea
g
una forma bilineal simétrica definida positiva (si el cuerpo es

) o una forma hermítica
(si el cuerpo es
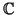
). Sea

una forma bilineal simétrica sobre
E. Existe una base
ortonormal para
g que es ortogonal para

. Es decir, existe una base de
E para la cual la matriz
de
g es la identidad y la de

es diagonal.
Recordemos, antes de demostrarlo, un concepto esencial en el estudio de la forma canónica de los endomorfismos.
Definición 4.1.2
Sea
V un espacio vectorial y
f :
V 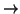 V
V un endomorfismo. Sea

un autovalor de
f. El
subespacio invariante asociado a 
es el subespacio vectorial
F(
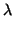
) = ker(
f -
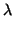 Id
Id )
ker(
f -
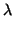 Id
Id )
2  ...
...
que es un subespacio de
V invariante y (recuerdo) admite una base
(
u1,...,
uk) con
f (
u1) =
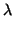 u1
u1,
f (
u2) =
u1 +
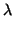 u2
u2, ...,
f (
uk) =
uk-1 +
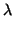 uk
uk.
LEMA 4.1.3
Sea
E un espacio vectorial real de dimensión finita, dotado de la forma bilineal simétrica definida
positva
g. Sea
f :
E 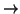 E
E un endomorfismo. Supongamos que la matriz de
f en una base

ortonormal para
g es
simétrica, y sean

,

dos autovalores de
f, reales y
distintos. Entonces los subespacios
propios asociados a

y

son mutuamente ortogonales para
g.
Demostración.
Fijamos la base

del enunciado, en la cual la matriz de
g es la identidad y la de
f es
simétrica. Sean
V(

) y
V(

) los subespacios propios asociados a

y

,
respectivamente. Consideremos en
E la forma bilineal simétrica
H cuya matriz en

es
la misma que la de
f y sean
u  V
V(

) y
v  V
V(

) dos vectores no nulos de los subespacios
respectivos. Hemos de comprobar que
g(
u,
v) = 0. En la base

, los vectores se escribirán
u = (
u1,...,
un) y
v = (
v1,...,
vn) y es
f (
u) =
 u
u,
f (
v) =
 v
v. Por un lado se
tiene que
H(
u,
v) = (
u1 ... un)
M
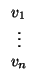

= (
u1 ... un)
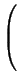
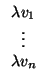
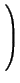
=
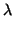 g
g(
u,
v),
la última igualdad porque

es una base ortonormal para
g. Por otro lado, fijándonos
en ``la parte izquierda'' y razonando igual,
H(
u,
v) = (
u1 ... un)
M
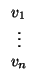

= (
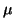 u1 ...
u1 ... 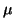 un
un)

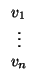

=
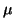 g
g(
u,
v).
De donde
 g
g(
u,
v) =
 g
g(
u,
v). Como

y

son distintos, ha de ser
g(
u,
v) = 0: es
decir,
u y
v son ortogonales para
g.

LEMA 4.1.4
Sea (
E,
g) un espacio métrico real de dimensión finita. Sea
f :
E  E
E un endomorfismo que
en una base

ortonormal, es simétrico y sea

un valor propio real de
f. Entonces
el subespacio invariante
F(

) es igual al subespacio propio
V(

) y, por tanto, existe
una base de
F(

) formada por vectores propios.
Demostración.
Hemos de demostrar que el espacio propio del autovalor

es igual a
F(

). Si no lo fuera, por el
teorema de Jordan existirían dos vectores no nulos
u,
v  F
F(

) tales que
f (
u) =
 u
u y
f (
v) =
u +
 v
v. Escribiendo, como en el lema anterior,
u = (
u1,...,
un) y
v = (
v1,...,
vn), se
tendría, por un lado
H(u, v) = (u1 ... un)M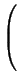 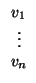  |
= (u1 ... un) 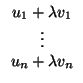 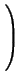 = = |
|
| |
= g(u, u + 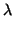 v) = g(u, u) + v) = g(u, u) + 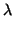 g(u, v), g(u, v), |
|
y por otro,
H(
u,
v) = (
u1 ... un)
M
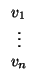

= (
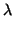 u1 ...
u1 ... 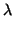 un
un)

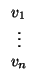

=
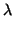 g
g(
u,
v),
de donde
g(
u,
u) +
 g
g(
u,
v) =
 g
g(
u,
v), es decir,
g(
u,
u) = 0, que contradice el hecho de que
g
es una métrica (por tanto, definida) y que
u 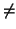
0.

LEMA 4.1.5
Los valores propios de un endomorfismo
f de un espacio vectorial real cuya matriz en alguna base

es
simétrica, son todos reales.
Demostración.
Supongamos que no. Entonces
f tiene dos autovalores complejos conjugados,

y
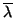
. El subespacio
F = ker(
f2 - 2
Re(

)
f +|

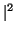 Id
Id es invariante
(compruébese). Se sabe (Jordan real) que en
F hay dos vectores
u,
v no nulos tales que
f (
u) =
Re(

)
u -
Im(

)
v y
f (
v) =
Im(

)
u +
Re(

)
v. Por otro lado, como la matriz
M de
f en

es simétrica, si escribimos
u = (
u1,...,
un) y
(
v1,...,
vn) y
consideramos el producto escalar usual en la base

, se tiene que
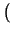 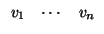  M M 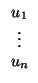  |
=  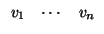  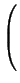 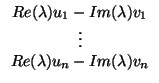 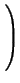 = = |
|
| |
= Re( ) < u, v > - Im( ) < u, v > - Im(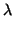 )|v )|v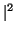 , , |
|
mietras que, ``por el otro lado'',
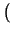 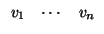  M M 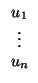  |
= |
|
= 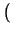 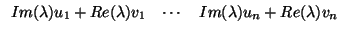  |
 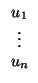  = = |
|
= Re(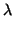 ) < u, v > + Im( ) < u, v > + Im(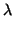 ) ) |
|v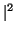 |
|
de donde
y, puesto que
u,
v 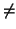
0, ha de ser
Im(

) = 0, contradicción.

Estamos ya en condiciones de demostrar el teorema 1.1.
Demostración.
Demostración del Teorema
1.1.
Partimos, como se dice en el enunciado, de un espacio métrico (
E,
g) y de una forma bilineal
simétrica

en
E (sólo vamos a probar el resultado en el caso real). Fijemos una base

de
E que sea ortonormal para
g. Puesto que

es simétrica, su matriz en

es una matriz simétrica; llamémosla
M. Sabemos también, por el lema
1.5, que sus autovalores son todos reales.
Olvidémonos por un momento de que M es la matriz de una forma bilineal y consideremos el endomorfismo
f de E cuya matriz asociada en la base
 es
M(f,
es
M(f, ) = M. Sean
{
) = M. Sean
{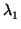 ,...,
,...,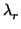 } los autovalores de f y
F(
} los autovalores de f y
F(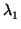 ),..., F(
),..., F(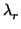 ) los
subespacios invariantes asociados a los valores propios. Por el lema 1.4
sabemos que
F(
) los
subespacios invariantes asociados a los valores propios. Por el lema 1.4
sabemos que
F(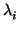 ) = V(
) = V(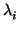 ) para todo i, es decir, que los subespacios invariantes
son los subespacios propios. Por el lema 1.3, los
F(
) para todo i, es decir, que los subespacios invariantes
son los subespacios propios. Por el lema 1.3, los
F(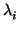 ) son
ortogonales dos a dos respecto de g. Si
) son
ortogonales dos a dos respecto de g. Si
 1,...,
1,..., r son bases de
F(
r son bases de
F(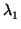 ),..., F(
),..., F(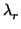 ) y cada una de ellas es ortogonal para g, entonces la base
) y cada una de ellas es ortogonal para g, entonces la base

 =
=  1
1 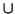 ...
... 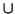
 r es una base ortogonal para g. Y,
evidentemente, si son ortonormales, también lo es
r es una base ortogonal para g. Y,
evidentemente, si son ortonormales, también lo es

 . Fijémonos en un subespacio
F(
. Fijémonos en un subespacio
F(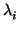 ). Como
F(
). Como
F(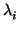 ) = V(
) = V(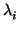 ), todos sus vectores son propios. Como g es
definida positiva en todo E, también lo es en
F(
), todos sus vectores son propios. Como g es
definida positiva en todo E, también lo es en
F(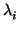 ), así que existe una base de
F(
), así que existe una base de
F(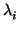 ) ortonormal para g: llamémosla
) ortonormal para g: llamémosla
 i. Sea
i. Sea

 la base
formada uniendo todas las
la base
formada uniendo todas las
 i. Esta
i. Esta

 es ortonormal para g y,
evidentemente, diagonaliza f: si
P = (pij) es la matriz de cambio de base de
es ortonormal para g y,
evidentemente, diagonaliza f: si
P = (pij) es la matriz de cambio de base de
 a
a

 , se tiene que
, se tiene que
Id = tP . IdP
por ser ambas bases ortonormales para
g y que
P-1M(
f,
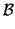
)
P =
D
donde
D es una matriz diagonal.
Ahora bien, por la primera igualdad, resulta que
P-1 = tP y, por tanto,
tPMP = D
(con
D diagonal). Pero, puesto que
M es la matriz de

en la base

y
P es
una matriz de cambio, esto significa que


es una base ortogonal para

, que es lo
que queríamos construir.




Next: Formas canónicas de las
Up: Resultados generales
Previous: Resultados generales
Pedro Fortuny Ayuso
2001-06-15
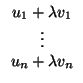
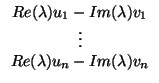
![]() es
M(f,
es
M(f,![]() ) = M. Sean
{
) = M. Sean
{![]() ,...,
,...,![]() } los autovalores de f y
F(
} los autovalores de f y
F(![]() ),..., F(
),..., F(![]() ) los
subespacios invariantes asociados a los valores propios. Por el lema 1.4
sabemos que
F(
) los
subespacios invariantes asociados a los valores propios. Por el lema 1.4
sabemos que
F(![]() ) = V(
) = V(![]() ) para todo i, es decir, que los subespacios invariantes
son los subespacios propios. Por el lema 1.3, los
F(
) para todo i, es decir, que los subespacios invariantes
son los subespacios propios. Por el lema 1.3, los
F(![]() ) son
ortogonales dos a dos respecto de g. Si
) son
ortogonales dos a dos respecto de g. Si
![]() 1,...,
1,...,![]() r son bases de
F(
r son bases de
F(![]() ),..., F(
),..., F(![]() ) y cada una de ellas es ortogonal para g, entonces la base
) y cada una de ellas es ortogonal para g, entonces la base
![]()
![]() =
= ![]() 1
1 ![]() ...
... ![]()
![]() r es una base ortogonal para g. Y,
evidentemente, si son ortonormales, también lo es
r es una base ortogonal para g. Y,
evidentemente, si son ortonormales, también lo es
![]()
![]() . Fijémonos en un subespacio
F(
. Fijémonos en un subespacio
F(![]() ). Como
F(
). Como
F(![]() ) = V(
) = V(![]() ), todos sus vectores son propios. Como g es
definida positiva en todo E, también lo es en
F(
), todos sus vectores son propios. Como g es
definida positiva en todo E, también lo es en
F(![]() ), así que existe una base de
F(
), así que existe una base de
F(![]() ) ortonormal para g: llamémosla
) ortonormal para g: llamémosla
![]() i. Sea
i. Sea
![]()
![]() la base
formada uniendo todas las
la base
formada uniendo todas las
![]() i. Esta
i. Esta
![]()
![]() es ortonormal para g y,
evidentemente, diagonaliza f: si
P = (pij) es la matriz de cambio de base de
es ortonormal para g y,
evidentemente, diagonaliza f: si
P = (pij) es la matriz de cambio de base de
![]() a
a
![]()
![]() , se tiene que
, se tiene que