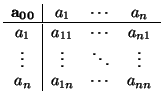
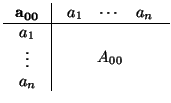
C 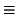 a00 + 2
a00 + 2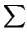 aixi +
aixi + 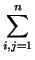 aijxixj = 0,
aijxixj = 0,
donde
aij = aji y algún aij es distinto de 0. Geométricamente, una cuádrica es
``el conjunto de puntos del espacio euclídeo que satisfacen una ecuación como C'' -pero esta
definición es engañosa (ver notas de clase).