Demostración.
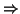
) Tales simetrías consisten únicamente en cambiar de signo la coordenada
i -ésima
de los puntos de
E. Por tanto, si
c = 0, la ecuación de
C sólo tiene términos de segundo grado
y, por tanto, no se ve afectada por cambios de signo.
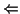 ) Supongamos que c
) Supongamos que c 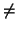 0. La simetría de eje xr+1 = 0 consiste en cambiar de signo
la coordenada r + 1 -ésima. Como es una ecuación de segundo grado estricto,
0. La simetría de eje xr+1 = 0 consiste en cambiar de signo
la coordenada r + 1 -ésima. Como es una ecuación de segundo grado estricto,
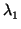
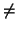 0. Entonces, el punto
0. Entonces, el punto
 = (1, 0,..., pr+1 = -
= (1, 0,..., pr+1 = - 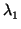 /c, 0,..., 0) cumple la ecuación, pero
su imagen por la simetría, que es
/c, 0,..., 0) cumple la ecuación, pero
su imagen por la simetría, que es
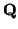 = (1, 0,..., pr+1 =
= (1, 0,..., pr+1 = 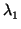 /c, 0,..., 0) no.
/c, 0,..., 0) no.
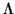
Definición 4.1.20
Una cuádrica es
un cilindro si
-
rg(A00) < n y C tiene centro, o bien
-
rg(A00) < n - 1 y C no tiene centro.
Es interesante demostrar (como ejercicio) que una cónica es un cilindro si y sólo si existe un plano
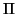
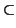 E
E de vector director
v que cumple la siguiente condición: para todo punto

de
C, la recta

+ <
v > corta a
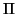
en un punto de
C (ésta es la noción ``precisa'' de cilindro'').
![]() ) Supongamos que c
) Supongamos que c ![]() 0. La simetría de eje xr+1 = 0 consiste en cambiar de signo
la coordenada r + 1 -ésima. Como es una ecuación de segundo grado estricto,
0. La simetría de eje xr+1 = 0 consiste en cambiar de signo
la coordenada r + 1 -ésima. Como es una ecuación de segundo grado estricto,
![]()
![]() 0. Entonces, el punto
0. Entonces, el punto
![]() = (1, 0,..., pr+1 = -
= (1, 0,..., pr+1 = - ![]() /c, 0,..., 0) cumple la ecuación, pero
su imagen por la simetría, que es
/c, 0,..., 0) cumple la ecuación, pero
su imagen por la simetría, que es
![]() = (1, 0,..., pr+1 =
= (1, 0,..., pr+1 = ![]() /c, 0,..., 0) no.
/c, 0,..., 0) no.
![]()