


Next: Cuádricas con y sin
Up: Formas canónicas de las
Previous: Formas canónicas de las
. Para clasificar las
cuádricas de un espacio euclídeo, vamos a permitir realizar cambios de referencia (o, lo que es lo
mismo, movimientos). En realidad, vamos a restringirnos a los movimientos directos, puesto que se
obtienen los mismos resultados que permitiendo simetrías. Fijemos, pues, un espacio euclídeo
E de dimensión n y una referencia
 = (
= (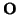 ,(e1,..., en)). Sea
C = a00 + 2
,(e1,..., en)). Sea
C = a00 + 2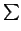 aixi +
aixi + 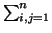 aijxixj una cuádrica en E con matriz
M(C,
aijxixj una cuádrica en E con matriz
M(C, ) = M. Puesto que todo
movimiento es composición de uno que deja fijo
) = M. Puesto que todo
movimiento es composición de uno que deja fijo 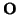 y una traslación, estudiamos primero el comportamiento
por movimientos que fijan
y una traslación, estudiamos primero el comportamiento
por movimientos que fijan 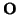 y después por traslaciones.
y después por traslaciones.
LEMA 4.1.7
Sea
f un movimiento de
E que deja fijo
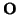
y
G su matriz asociada en

. Sea


la referencia obtenida al aplicarle
f a

. Escribamos
Entonces, la matriz de
C en la referencia


es
donde
Demostración.
Basta tener en cuenta que, si
(
x'1,...,
x'n) son las coordenadas de
(
x1,...,
xn) en la
nueva referencia, entonces
y sustituir esta expresión en la ecuación de la cuádrica
C dada en la referencia

.

De este resultado y del teorema de diagonalización simultánea de métrica y forma bilineal
simétrica, se deduce inmediatamente el siguiente
TEOREMA 4.1.8
Existe un cambio de referencia en
E que deja fijo el origen, que transforma la matriz de
C en una matriz
donde
D00 es una matriz diagonal.
Demostración.
Como ya hemos visto, los movimientos que dejan fijo el origen afectan a la matriz
A00 como los
cambios de una base ortonormal a otra. Aplicando el teorema de diagonalización simultánea, puesto que
A00 es diagonal, se termina.

LEMA 4.1.9
En el teorema anterior, si f es una simetría que deja fijo el origen (es decir, f2 = Id),
entonces existe un movimiento
directo g que también deja fijo el origen y que transforma la ecuación de C en
la misma ecuación en que la transforma f.
Demostración.
Si
f es tal simetría y

su isometría asociada, entonces

transformará
la base

= (
e1,...,
en) en la base


= (
e'1 =

(
e)
1,...,
e'n =

(
en)). Basta tomar el movimiento
g que deja fijo
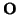
y cuya isometría es
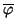
que cumple:
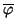
(
e1) = -
e'1 y
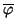
(
ei) =
e'i, para
i = 2,...,
n. Téngase en cuenta que si una isometría es una
simetría, es porque el determinante de la matriz asociada es -1; para cambiar el signo, basta
cambiar de signo una columna: eso es lo que se hace al tomar, en vez de
e'1, su opuesto. La
operación es ``cambiar de signo la primera coordenada'' y, como la matriz de
C tras
f es diagonal,
es
C 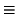 a00
a00 + 2
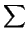 a'ixi
a'ixi +
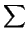 aiixi2
aiixi2 = 0,(
sin ``j'')
y un punto
(
x1,...,
xn) cumple esa ecuación si y sólo si
(-
x1,
x2,...,
xn) la cumple.

Nota 4.1.10
De hecho, lo que se tiene es que se puede diagonalizar simultáneamente una métrica y una forma
bilineal simétrica con una isometría que sea una rotación (es decir, de determinante +1). La
demostración es la del lema anterior.
LEMA 4.1.11
Dada una cuádrica
C en el espacio euclídeo
E, en una referencia

, si
g es una
traslación de vector
v = (
v1,...,
vn) y la matriz de
C es
M =
M(
C,

) (con la
notación de la sección anterior), entonces la
matriz de
C en la referencia


obtenida ``por el cambio''
g es
donde
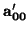
=
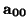
+ 2 <
v,
a > (
a es el vector
(
a1,...,
an) y
No lo demostramos porque es un ejercicio muy sencillo (téngase en cuenta que la isometría asociada
a una traslación es la identidad, cuya matriz es, en cualquier base, la misma).
De los dos lemas anteriores se deduce el
TEOREMA 4.1.12
[Primera forma canónica de una cuádrica]
Dada una cuádrica
C en una referencia

del espacio euclídeo
E, existe un
movimiento directo (es decir, un cambio de referencia que conserva la orientación)
g de
E tal que
la matriz de
C en la referencia


=
g(

) es de la forma
donde los
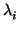
son todos distintos de 0.
Demostración.
Que la matriz
A00 se puede transformar en una diagonal con los autovalores distintos de 0 en los
primeros lugares es consecuencia del teorema de diagonalización simultánea y de la nota anterior. Una
vez escrita así la cuádrica, los autovalores no nulos eliminan -mediante una traslación
conveniente- los términos
aj que corresponden, sin afectar a la parte de grado 2. Los otros (los
ci que aparecen), en principio no podemos eliminarlos (aunque veremos a continuación que ``casi'').

En realidad, el resultado se puede refinar aún más:
TEOREMA 4.1.13
[Forma canónica de una cuádrica]
Dada una cuádrica
C en una referencia

de
E, existe una referencia


en
la que su matriz es
donde, si
c'1 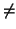
0, entonces
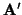
= 0 y los
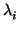
son todos distintos de 0.
Demostración.
Tómese una referencia



= (
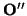
,(
e''1,...,
e''n)) en la
que
C se escriba como en el
Teorema
1.12. Si
ci = 0 para todo
i, entonces tomamos


=



y se termina (en este caso,
c1 = 0 también). Si no, podemos suponer que
c1 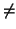
0 en la expresión del Teorema
1.12 (tras, eventualmente,
cambiar de orden dos vectores de la base y de signo uno de ellos). Consideremos el vector
(
c1,...,
cn-r) del espacio euclídeo
n -
r dimensional
En-r. Existe por lo menos un movimiento
directo
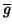
de
En-r que lo transforma en el vector
(
c'1, 0,..., 0), con
|(
c1,...,
cn-r)|=|
c'1|. Si
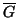
es la matriz de
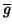
, se
toma el movimiento
g en
E de matriz
que es directo. Se comprueba inmediatamente que
g transforma la matriz de
C en la del enunciado (por
el lema de la sección anterior sobre el efecto de las rotaciones en la matriz de una cuádrica). Para
terminar, en este caso (
c'1 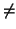
0) se puede cambiar de referencia por la traslación
x'n+1 =
x'n+1 -
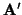
/
c'1 y se elimina el
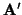
.

La forma matricial del Teorema 1.13 se llama matriz canónica de la
cuádrica C. La ecuación
se llama forma canónica de C.
Definición 4.1.14
Sea
C una cuádrica cuya forma canónica es
Se llama
ecuación reducida de C a la siguiente ecuación:
- Si A' = 0, entonces la forma canónica es ya la ecuación reducida.
- Si A'
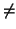 0, entonces la ecuación reducida de C es
0, entonces la ecuación reducida de C es
±1 +
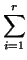
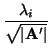 xi2
xi2 = 0,
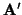 .
.
Es obvio que la ecuación reducida es la misma que la forma canónica (pues se han dividido ambos
miembros por el mismo número). Para terminar, se tiene el
TEOREMA 4.1.15 (de clasificación de cuádricas)
Dos cuádricas difieren en un cambio de referencia si y sólo si tienen la misma ecuación reducida
(salvo cambio de orden de las variables).
La demostración es consecuencia de todos los resultados previos. Terminamos dando una lista de
invariantes para una cuádrica:
TEOREMA 4.1.16
Dada una cuádrica de matriz
M en una referencia ortonormal


, los siguientes números
son invariantes (no dependen de la referencia ortonormal):
- El rango de A00.
- El rango de M.
- La signatura de A00.
La demostración de que son invariantes es, una vez más, consecuencia de todo el trabajo que ya hemos hecho.



Next: Cuádricas con y sin
Up: Formas canónicas de las
Previous: Formas canónicas de las
Pedro Fortuny Ayuso
2001-06-15
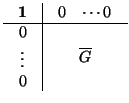
 .
.
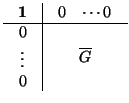
 ) =
) = 
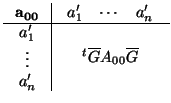
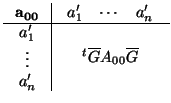
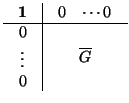
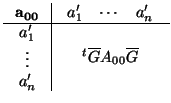
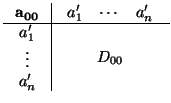
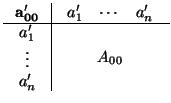


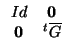
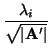 xi2 = 0,
xi2 = 0,