


Next: Propiedades del ortogonal.
Up: FORMAS BILINEALES
Previous: Matriz de una forma
En todo este capítulo trataremos con formas bilineales simétricas. (Ej: el producto escalar).
Definición 1.2.1
Sea
f una forma bilineal simétrica sobre un e.v.
V.
- Dos vectores u, v se llaman ortogonales (y se escribe)
u
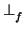 v si y sólo si
f (u, v) = 0. Por lo general no escribiremos la f, porque se sobreentenderá.
v si y sólo si
f (u, v) = 0. Por lo general no escribiremos la f, porque se sobreentenderá.
- Si
S
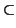 V es un subconjunto de V, se llama variedad ortogonal a S y se escribe
S
V es un subconjunto de V, se llama variedad ortogonal a S y se escribe
S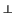 a
a
Ejemplos:
- Para el producto escalar habitual en
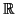 3, los vectores (1, 1, 1) y (0, - 1, 1) (dibujarlos)
son ortogonales. Para esta forma no hay vectores isótropos aparte del 0.
3, los vectores (1, 1, 1) y (0, - 1, 1) (dibujarlos)
son ortogonales. Para esta forma no hay vectores isótropos aparte del 0.
- Para la forma que tiene las mismas ecuaciones pero en
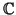 3, el vector (1, i, 0) es
ortogonal a sí mismo.
3, el vector (1, i, 0) es
ortogonal a sí mismo.
Se define vector isótropo como aquél que es ortogonal a sí mismo. Por ejemplo, en Relatividad,
la forma cuadrática que se utiliza es
x12 + x22 + x32 - x42 y los vectores isótropos
son aquellos que tienen ``mismo espacio y tiempo'' en módulo, v. gr.:
(0, 1, 0, 1), (1, 1, 1,
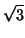
),...
PROPOSICIÓN 1.2.2
Dada una forma bilineal simétrica sobre un e.v.
V, se tiene:
ker(
f )=
V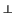
.
LEMA 1.2.3
Dos vectores no isótropos y ortogonales son linealmente independientes.
Demostración.
Tomemos una combinación lineal e igualémosla a 0:
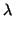 u
u +
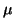 v
v = 0.
Apliquemos la condición:
f (
u,
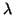 u
u +
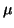 v
v) =
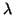 f
f (
u,
u) +
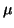 f
f (
u,
v) =
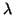 f
f (
u,
u) pues son
ortogonales. Como
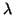 u
u +
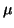 v
v = 0, es
f (
u,
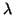 u
u +
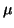 v
v) =
f (
u, 0) = 0. Ergo
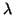 f
f (
u,
u) = 0 y, por
ello,
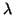
= 0, pues
u no es isótropo. Lo mismo para
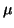
.
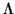
PROPOSICIÓN 1.2.4
Una forma bilineal simétrica es definida si y sólo si el único vector isótropo es el 0.
Demostración.
Para la derecha es evidente y para la izquierda también.
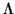
Subsecciones



Next: Propiedades del ortogonal.
Up: FORMAS BILINEALES
Previous: Matriz de una forma
Pedro Fortuny Ayuso
2001-06-15
 v si y sólo si
f (u, v) = 0. Por lo general no escribiremos la f, porque se sobreentenderá.
v si y sólo si
f (u, v) = 0. Por lo general no escribiremos la f, porque se sobreentenderá.
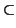 V es un subconjunto de V, se llama variedad ortogonal a S y se escribe
S
V es un subconjunto de V, se llama variedad ortogonal a S y se escribe
S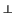 a
S
a
S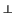 = {v
= {v 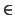 V : u
V : u 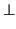 v
v 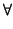 u
u 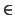 S}
S}