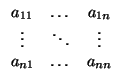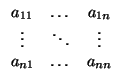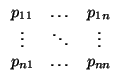Next: Ortogonalidad, etc...
Up: Introducción
Previous: Definición de forma cuadrática
Vamos a escribir las cosas como trabajan los humanos, esto es, con ``numeritos''.
PROPOSICIÓN 1.1.13
Sea
V un espacio vectorial de dimensión
n sobre un cuerpo
K y
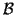
= (
e1,...,
en) una
base de
V. Sea (
aij) una matriz
n×
n de elementos de
K. Con estos datos, existe una única
forma bilineal
f :
V×
V 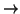 K
K tal que
f (
ei,
ej) =
aij para todos los
i,
j de 1 a
n.
Demostración.
Primero la existencia y luego la unicidad
- Existencia. Pues, dados u, v
 V, los escribo
V, los escribo
u =
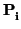 e1
e1 + ... +
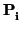 en
en,
v =
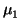 e1
e1 + ...
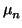 en
en
y defino
y ``se comprueba'' que esto es bilineal.
- Unicidad. Es evidente, porque si queremos que sea bilineal, dados u, v
 V, escritos en la base
V, escritos en la base
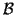 , la expresión de f (u, v) debe ser la de arriba.
, la expresión de f (u, v) debe ser la de arriba.
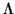
Así pues, podemos hablar de la matriz de una forma bilineal en la base
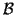 . Tal como lo
hemos escrito arriba, se pone
que, más abreviadamente, si llamamos M a la matriz (aij), escribimos
. Tal como lo
hemos escrito arriba, se pone
que, más abreviadamente, si llamamos M a la matriz (aij), escribimos
f (u, v) = utMv.
Es evidente que una forma bilineal es simétrica si y sólo si hay una base en la cual la matriz es
simétrica, es decir M = Mt y es hemisimétrica si y sólo si M = - Mt (y en ambos casos, todas lo
cumplen).
Para formas hermíticas, lo de arriba se escribe
y, además,
aij = 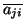 .
.
HASTA AQUÍ LA CLASE 2: 990211
PROPOSICIÓN 1.1.14
La matriz de
f depende de la base elegida. En concreto, si
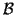
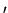
= (
e'1,...,
e'n) es otra
base y el cambio de base viene dado por la matriz
P (esto es:
P = (
pij) y se pone
e'i =
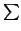 pjiej
pjiej)
(atención a los subíndices pij en P y pji en e'i), entonces la
matriz de
f en la base
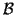
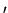
es
PtMP.
Demostración.
donde las
vi son las coordenadas en la base
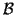
y las
v'i en la base
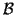
. Para
u, como lo estamos poniendo traspuesto, es
(u1 ... un) = (u'1 ... u'n)Pt
de donde:
f (
u,
v) = (
u'1 ... u'n)
PtMP
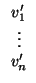
.
Importante: para formas hermíticas -en las que
f (
u,
v) =
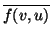
y lineales en la
primera- el cambio de base es: MUCHO OJO CON ESTO!:
f (
u,
v) = (
u1 ... un)
PtM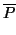
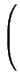
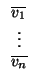
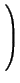
; i.e.
M' =
PtM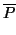
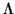
Primer invariante asociado a una matriz de una forma bilineal: Supongamos que nuestra forma f
es simétrica, antisimétrica o hermítica. Entones el núcleo ker(f ) está bien definido y tiene
dimensión r, por ejemplo. Sea M una matriz de f en una base cualquiera. Un vector v está en el
núcleo si y sólo si la aplicación
f ( . , v) es exactamente la aplicación 0. Ergo si y sólo si
es decir, si es solución del sistema homogéneo que define M. Pero las soluciones de este sistema
homogéneo son un subespacio vectorial de V de dimensión
n - rg(M). De donde
n - rg(M) = dim(ker(f )).
Problemas: ¿dónde he utilizado que f sea simétrica? Hacer esta demostración para las
hermíticas.
HASTA AQUÍ LA CLASE 3 990212



Next: Ortogonalidad, etc...
Up: Introducción
Previous: Definición de forma cuadrática
Pedro Fortuny Ayuso
2001-06-15