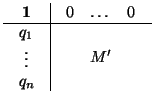Next: Las simetrías
Up: Isometrías y Movimientos.
Previous: Movimientos de un espacio
Ya hemos visto en el lema 3.6 que la composición de isometrías es una
isometría y que la composición de movimientos es un movimiento. Es evidente que la composición de
isometrías (respectivamente, de movimentos) cumple la propiedad asociativa. La identidad es una
isometría (respectivamente, un movimento). Que el inverso de una isometría es una isometría es
una comprobación elemental: suponiendo que
 : V
: V 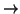 V es una isometría, su inverso
V es una isometría, su inverso
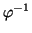 lo es porque dados u, v
lo es porque dados u, v  V y tomadas sus imágenes por
V y tomadas sus imágenes por
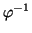 ,
,
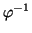 (u),
(u),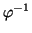 (v), se tiene que (al ser
(v), se tiene que (al ser  una isometría):
una isometría):
<
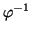
(
u),
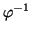
(
v) > = <
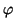
(
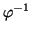
(
u)),
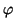
(
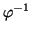
(
v)) > = <
u,
v > ,
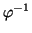 es una isometría. De aquí se deduce inmediatamente que el inverso de
un movimiento es un movimiento (recuérdese que el inverso de una afinidad es una afinidad y que una afinidad
es un movimiento si y sólo si su automorfismo asociado es la identidad, etc.). Así pues, tanto las
isometrías de un espacio métrico como los movimientos de un espacio euclídeo, forman un grupo. El
grupo de las isometrías de (V, g) se llama grupo ortogonal de V. Si V es
es una isometría. De aquí se deduce inmediatamente que el inverso de
un movimiento es un movimiento (recuérdese que el inverso de una afinidad es una afinidad y que una afinidad
es un movimiento si y sólo si su automorfismo asociado es la identidad, etc.). Así pues, tanto las
isometrías de un espacio métrico como los movimientos de un espacio euclídeo, forman un grupo. El
grupo de las isometrías de (V, g) se llama grupo ortogonal de V. Si V es
 n, se
llama grupo ortogonal n -dimensional real. Se denotan
n, se
llama grupo ortogonal n -dimensional real. Se denotan
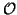 (V) y
(V) y
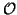 n(
n( ). El grupo de
movimientos de E se denota Mov(E).
). El grupo de
movimientos de E se denota Mov(E).
Ya hemos visto que, fijada una base
(e1,..., en) ortonormal en V, el grupo ortogonal de
V es isomorfo al
grupo de matrices cuadradas n×n cuyas matrices inversa y traspuesta coinciden. Puesto que todo
movimiento es composición de una traslación y un movimiento que deja fijo un punto, es claro que, una vez
tomada una referencia ortonormal, el grupo de movimientos de un espacio euclídeo E es igual al grupo de
matrices del tipo
donde M' es la matriz de una isometría, es decir,
M'-1 = M't. De aquí se deduce que todo
movimiento es composición de una traslación y de un movimiento que deja fijo un punto.
Definición 3.3.8
Diremos que una isometría es una rotación si conserva la orientación. En términos
matriciales, una isometría es una rotación si el determinante de su matriz en cualquier base es
positivo. Si hemos fijado una base ortonormal, entonces una isometría es una rotación si y sólo si
su determinante es +1. Diremos que un movimiento es directo si su isometría asociada es una
rotación. Es evidente que las traslaciones son movimientos directos (su isometría asociada es la identidad).



Next: Las simetrías
Up: Isometrías y Movimientos.
Previous: Movimientos de un espacio
Pedro Fortuny Ayuso
2001-06-15