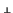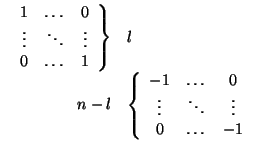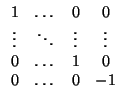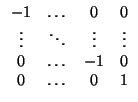Las simetrías

Definición 3.3.9   La simetría de un espacio vectorial métrico V respecto de un subespacio L es la aplicación S_L : V 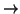$\rightarrow$ V siguiente:

S_L(v) = v - 2v_L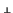^$\perp$

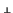
donde v_L^$\perp$ es la componente vertical de v respecto de L. Si L = {0}, entonces la simetría S_{0} es exactamente S_{0}(v) = - v.

PROPOSICIÓN 3.3.10   Toda simetría de un espacio métrico es una isometría.

Demostración. Sea $\varphi$ la simetría de V respecto de L. Sea (e₁,..., e_l) una base ortonormal de L (si L = {0} entonces l = 0 y no hacemos nada). Sea (e_l+1,..., e_n) una base ortonormal de L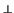^$\perp$ (si L = {0} entonces L^$\perp$ = V y tomamos una base ortonormal de V). El conjunto (e₁,..., e_n) es una base de V. Calculemos la matriz de $\varphi$ en esta base. Por definición $\varphi$(e_i) = e_i para i = 1...l, mientras que $\varphi$(e_j) = e_j - 2e_j = - e_j para j = l + 1,..., n. Por tanto, la matriz N de $\varphi$ en (e₁,..., e_l) es

N = $$\left(\vphantom{ \begin{array}{rl} \left. \begin{array}{ccc} 1 &... ...ots & \ddots & \vdots\\ 0 & \dots & -1 \end{array}\right. \end{array}}\right.$$$$\begin{array}{rl} \left. \begin{array}{ccc} 1 & \dots & 0\\ \v... ...\\ \vdots & \ddots & \vdots\\ 0 & \dots & -1 \end{array}\right. \end{array}$$$$\left.\vphantom{ \begin{array}{rl} \left. \begin{array}{ccc} 1 &... ...ots & \ddots & \vdots\\ 0 & \dots & -1 \end{array}\right. \end{array}}\right)$$

que es claramente la matriz de una isometría, pues N^-1 = N y N^t = N, de donde N^-1 = N^t. $\qedsymbol$

Nota 3.3.11   De la demostración se deduce que si L es un hiperplano y (e₁,..., e_n) es una base ortonormal tal que L = < e₁,..., e_n-1 >, entonces la matriz de la simetría S_L en dicha base es

$$\left(\vphantom{ \begin{array}{cccc} 1 & \dots & 0 & 0\\ \vdots... ...vdots & \vdots\\ 0 & \dots & 1 & 0\\ 0 & \dots & 0 & -1 \end{array}}\right.$$$$\begin{array}{cccc} 1 & \dots & 0 & 0\\ \vdots & \ddots & \vdots & \vdots\\ 0 & \dots & 1 & 0\\ 0 & \dots & 0 & -1 \end{array}$$$$\left.\vphantom{ \begin{array}{cccc} 1 & \dots & 0 & 0\\ \vdots... ...vdots & \vdots\\ 0 & \dots & 1 & 0\\ 0 & \dots & 0 & -1 \end{array}}\right)$$

y que si L es una recta vectorial y en una base ortonormal (e'₁,..., e'_n) el subespacio L es L = < e'_n >, entonces la ecuación de S_L en esa base es

$$\left(\vphantom{ \begin{array}{cccc} -1 & \dots & 0 & 0\\ \vdot... ...vdots & \vdots\\ 0 & \dots & -1 & 0\\ 0 & \dots & 0 & 1 \end{array}}\right.$$$$\begin{array}{cccc} -1 & \dots & 0 & 0\\ \vdots & \ddots & \vdots & \vdots\\ 0 & \dots & -1 & 0\\ 0 & \dots & 0 & 1 \end{array}$$$$\left.\vphantom{ \begin{array}{cccc} -1 & \dots & 0 & 0\\ \vdot... ...vdots & \vdots\\ 0 & \dots & -1 & 0\\ 0 & \dots & 0 & 1 \end{array}}\right)$$.