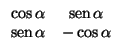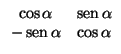Next: Isometrías de tipo a)
Up: Isometrías y Movimientos.
Previous: Las simetrías
Como hemos visto, todos los espacios métricos de dimensión n son isométricos. Por tanto, a la hora de
estudiar el grupo de isometrías, podemos trabajar siempre en
 n con el producto escalar usual
y con la base canónica, que es ortonormal para ese producto. Por eso el título se refiere a
n con el producto escalar usual
y con la base canónica, que es ortonormal para ese producto. Por eso el título se refiere a
 2, pero el estudio sirve para cualquier espacio de dimensión 2. Como, por otra parte, fijada una
base ortonormal, el grupo ortogonal
2, pero el estudio sirve para cualquier espacio de dimensión 2. Como, por otra parte, fijada una
base ortonormal, el grupo ortogonal
 (
( 2) es isomorfo al grupo de matrices 2×2
ortonormales, nos podemos limitar a estudiar el grupo de matrices
tales que su inversa es su traspuesta, es decir, tales que
o sea,
a112 + a212 = a122 + a222 = 1 y
a11a12 + a21a22 = 0.
2) es isomorfo al grupo de matrices 2×2
ortonormales, nos podemos limitar a estudiar el grupo de matrices
tales que su inversa es su traspuesta, es decir, tales que
o sea,
a112 + a212 = a122 + a222 = 1 y
a11a12 + a21a22 = 0.
Las dos primeras igualdades permiten elegir dos ángulos
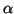 ,
,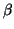 y escribir
a11 = cos
y escribir
a11 = cos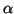 ,
a21 =
,
a21 = 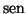
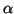 ,
a12 =
,
a12 = 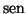
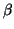 y
a22 = cos
y
a22 = cos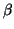 . Así las cosas, la segunda condición
se traduce por
. Así las cosas, la segunda condición
se traduce por
es decir,
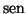 (
(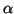 +
+ 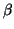 ) = 0, con lo cual
) = 0, con lo cual
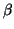 = -
= - 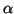 + (2k + 1)
+ (2k + 1) , ó
, ó
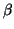 = -
= - 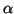 + 2k
+ 2k , donde k es un número entero. En todo caso,
sólo hay dos posibilidades esecialmente distintas (tomando k = 0):
, donde k es un número entero. En todo caso,
sólo hay dos posibilidades esecialmente distintas (tomando k = 0):
- a)
-
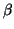 = -
= - 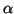 +
+  . Se tiene que
cos
. Se tiene que
cos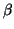 = - cos
= - cos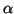 y
que
y
que
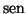
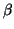 =
= 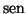
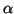 . Por tanto, la matriz es
cuyo determinante es -1: es una simetría.
. Por tanto, la matriz es
cuyo determinante es -1: es una simetría.
- b)
- En el otro caso,
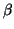 = -
= - 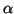 . Se tiene que
. Se tiene que
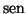
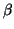 = -
= - 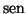
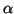 y que
cos
y que
cos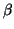 = cos
= cos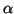 , de donde la matriz es
cuyo determinante es +1: es una rotación.
, de donde la matriz es
cuyo determinante es +1: es una rotación.
Vamos a estudiar con algo más de detalle cada tipo.
Subsecciones



Next: Isometrías de tipo a)
Up: Isometrías y Movimientos.
Previous: Las simetrías
Pedro Fortuny Ayuso
2001-06-15
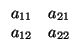
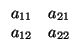
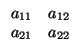
![]() ,
,![]() y escribir
a11 = cos
y escribir
a11 = cos![]() ,
a21 =
,
a21 = ![]()
![]() ,
a12 =
,
a12 = ![]()
![]() y
a22 = cos
y
a22 = cos![]() . Así las cosas, la segunda condición
se traduce por
. Así las cosas, la segunda condición
se traduce por