Isometrías de tipo b)

Dada una isometría $\varphi$ de tipo b), de matriz

M_$\varphi$ = $$\left(\vphantom{ \begin{array}{cc} \cos\alpha & \sen\alpha \\ -\sen\alpha & \cos\alpha \end{array}}\right.$$$$\begin{array}{cc} \cos\alpha & \sen\alpha \\ -\sen\alpha & \cos\alpha \end{array}$$$$\left.\vphantom{ \begin{array}{cc} \cos\alpha & \sen\alpha \\ -\sen\alpha & \cos\alpha \end{array}}\right)$$,

y dado un vector v = (v₁, v₂), el transformado de v por M_$\varphi$ es

$$\left(\vphantom{ \begin{array}{cc} \cos\alpha & \sen\alpha \\ -\sen\alpha & \cos\alpha \end{array}}\right.$$$$\begin{array}{cc} \cos\alpha & \sen\alpha \\ -\sen\alpha & \cos\alpha \end{array}$$$$\left.\vphantom{ \begin{array}{cc} \cos\alpha & \sen\alpha \\ -\sen\alpha & \cos\alpha \end{array}}\right)$$$$\left(\vphantom{ \begin{array}{c} v_{1}\\ v_{2} \end{array}}\right.$$$$\begin{array}{c} v_{1}\\ v_{2} \end{array}$$$$\left.\vphantom{ \begin{array}{c} v_{1}\\ v_{2} \end{array}}\right)$$ = (v₁cos$$\alpha$$ + v₂$$\sen$$$$\alpha$$, - v₁$$\sen$$$$\alpha$$ + v₂cos$$\alpha$$),

de modo que

< v,$$\varphi$$(v) > = (...) =|v$$\vert^{{2}}_{}$$cos$$\alpha$$,

es decir, $\varphi$ es exactamente^3.2el giro de ángulo ±$\alpha$. Para saber si es el ángulo positivo (+ $\alpha$) ó el negativo (- $\alpha$), se toma un caso particular: el vector e₁ de la base en la que trabajamos. Claramente $\varphi$(e₁) está rotado - $\alpha$ grados respecto de e₁, así que el giro es el negativo.

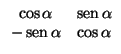
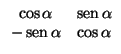
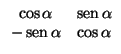
En resumen, las rotaciones del plano son exactamente los giros.

Por tanto, hemos demostrado el siguiente

TEOREMA 3.3.13   Las isometrías de $\mathbb {R}$² están formadas por los giros y las simetrías ortogonales. Una isometría es un giro si y sólo si conserva la orientación (i. e. su determinante es +1) y es una simetría si y sólo si cambia la orientación (i. e. su determinante es -1).

Pero aún hay más:

TEOREMA 3.3.14   Se tienen los siguientes enunciados:

1. Todo giro es composición de dos simetrías.
2. La composición de dos simetrías es un giro (que puede ser la identidad, si las dos simetrías son la misma).
3. Por tanto, el grupo ortogonal está generado por las simetrías axiales (toda isometría se puede escribir como composición de simetrías).

Demostración. 1) El giro de ángulo $\alpha$ (ojo, el ángulo $\alpha$) tiene (en una base ortonormal) asociada la matriz

$$\left(\vphantom{ \begin{array}{cc} \cos \alpha & -\sen \alpha \\ \sen \alpha & \cos \alpha \end{array}}\right.$$$$\begin{array}{cc} \cos \alpha & -\sen \alpha \\ \sen \alpha & \cos \alpha \end{array}$$$$\left.\vphantom{ \begin{array}{cc} \cos \alpha & -\sen \alpha \\ \sen \alpha & \cos \alpha \end{array}}\right)$$

Que es (compruébese) el producto de matrices siguiente:

$$\left(\vphantom{ \begin{array}{cc} \cos \alpha & -\sen \alpha \\ \sen \alpha & \cos \alpha \end{array}}\right.$$$$\begin{array}{cc} \cos \alpha & -\sen \alpha \\ \sen \alpha & \cos \alpha \end{array}$$$$\left.\vphantom{ \begin{array}{cc} \cos \alpha & -\sen \alpha \\ \sen \alpha & \cos \alpha \end{array}}\right)$$ = $$\left(\vphantom{ \begin{array}{cc} \cos\alpha & \sen\alpha \\ \sen\alpha & -\cos\alpha \end{array}}\right.$$$$\begin{array}{cc} \cos\alpha & \sen\alpha \\ \sen\alpha & -\cos\alpha \end{array}$$$$\left.\vphantom{ \begin{array}{cc} \cos\alpha & \sen\alpha \\ \sen\alpha & -\cos\alpha \end{array}}\right)$$$$\left(\vphantom{ \begin{array}{cc} 1 & 0\\ 0 & -1 \end{array}}\right.$$$$\begin{array}{cc} 1 & 0\\ 0 & -1 \end{array}$$$$\left.\vphantom{ \begin{array}{cc} 1 & 0\\ 0 & -1 \end{array}}\right)$$

(la simetría de eje y = 0 compuesta con la simetría de eje y = tan($\alpha$/2)x). Atención al orden porque es importante...

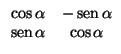
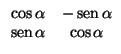
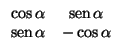
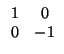
2) En una base ortonormal, el producto de dos simetrías de ejes respectivos y = tan($\alpha$/2)x y y = tan($\beta$/2)x es

$$\left(\vphantom{ \begin{array}{cc} \cos\alpha & \sen\alpha \\ \sen\alpha & -\cos\alpha \end{array}}\right.$$$$\begin{array}{cc} \cos\alpha & \sen\alpha \\ \sen\alpha & -\cos\alpha \end{array}$$$$\left.\vphantom{ \begin{array}{cc} \cos\alpha & \sen\alpha \\ \sen\alpha & -\cos\alpha \end{array}}\right)$$$$\left(\vphantom{ \begin{array}{cc} \cos \beta & \sen \beta \\ \sen \beta & -\cos \beta \end{array}}\right.$$$$\begin{array}{cc} \cos \beta & \sen \beta \\ \sen \beta & -\cos \beta \end{array}$$$$\left.\vphantom{ \begin{array}{cc} \cos \beta & \sen \beta \\ \sen \beta & -\cos \beta \end{array}}\right)$$ = $$\left(\vphantom{ \begin{array}{cc} \cos (\alpha-\beta) & -\sen (\alpha-\beta) \\ \sen (\alpha - \beta) & \cos (\alpha-\beta) \end{array}}\right.$$$$\begin{array}{cc} \cos (\alpha-\beta) & -\sen (\alpha-\beta) \\ \sen (\alpha - \beta) & \cos (\alpha-\beta) \end{array}$$$$\left.\vphantom{ \begin{array}{cc} \cos (\alpha-\beta) & -\sen (\alpha-\beta) \\ \sen (\alpha - \beta) & \cos (\alpha-\beta) \end{array}}\right)$$

que es el giro de ángulo $\alpha$ - $\beta$.

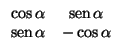
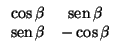
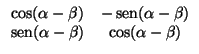
3) Se deduce directamente del 1) y el 2). $\qedsymbol$